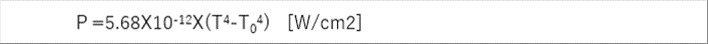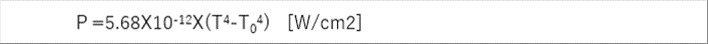| |
 |
 |
| ● 熱の伝わり方 |
| ● 製造現場の熱力学 |
| ● 基本的な量の定義 |
| 熱と温度 |
| 最大温度と最小温度 |
| 間違いやすい状態量の定義 |
| 温度の表記方法4つ |
| ● 熱輻射 Heat Radiation |
| ー 輻射率 |
| ー 黒体、灰体、白体 |
| ー キルヒホッフの法則 輻射エネルギーの吸収・反射 |
| ー 熱と絶対温度の関係 |
| ー 輻射率(放射率) |
| ー 輻射率の測定 |
| ● 熱伝達 Heat Transfer |
| 強制熱伝達率 |
| ● 熱伝導 Heat Conduction |
| ● 熱力学 |
| ● 気体の状態方程式 |
| ー 熱力学の3法則 |
| ー ニュートンの冷却の法則 |
| ー 冷却時の温度予測 |
| ー 熱伝達と温度境界層 |
| ー 熱伝導方程式, フーリエの法則 |
| |
 |
| ● 熱の伝わり方 |
| |
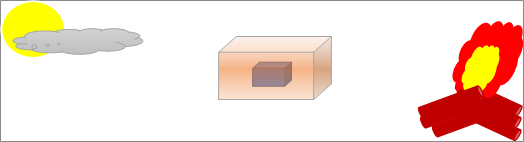
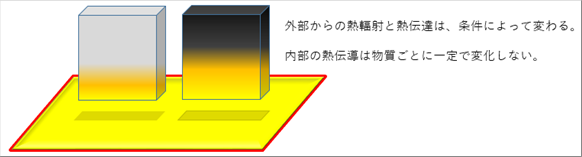
| 高温のものから低温の物に熱が伝わるが、この伝わり方には3種類あり、熱輻射、熱伝達、熱伝導である。日常生活ではどれをどう使ってもさほど困ることはないが、工業的にははっきり理解しておくことが望ましい。熱輻射、熱伝達、熱伝導は同時に発生するが、右下の絵で主体となる伝わり方が何かを把握しておきたい。 |
| |
| まず、熱はエネルギーなので、熱の伝わり方を、エネルギーの伝わり方と置き換えると考えやすいと思います |
| |
 |
| |
| 太陽の日差しは暖かいです。でも、曇りの日は太陽のありがたみをあまり感じません。また、電子レンジで冷凍食品をチンできます。キャンプなどの焚火は、煙が来ない風上の焚火からちょっと離れた場所でも暖かさを感じます。日差しが暖かいのは、エネルギーが真空中と空気中をつたわるからで、焚火の風上側で温まった空気が流れてこなくも暖かいのは、エネルギーが空気中を伝わるからです。曇りの日が温かくないのは、雲(水蒸気、水)でエネルギーが吸収されてしまうからです。これらは主に熱輻射によるものです。 |
| |
 |
| |
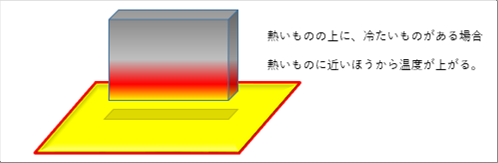
| 熱いものは、太陽、電子レンジ、焚火ですが、一般的な場合を考えてみます。熱いものの上に、冷たいものがあるとします。熱いものからのエネルギーの輻射に加えて、暖められた空気が上昇し、冷たいものに当たります。そのどちらもつめたいものの下面をメインに温めることになります。同時に、つめたいものの内部でも変化が起こります。内部には、直接輻射エネルギーも暖かい空気も直接届きせんが、下から上にエネルギーが伝わっていきます。側面も輻射エネルギーと暖かい空気があたるので、下部だけではなく、側面からも内部にエネルギーが伝わっていきます。 |
| |
| このように、熱エネルギーの伝わり方には、エネルギーの輻射、流体による伝達、物体内部の伝導の3通りあり、全体として、同時に起こっていることがわかると思います。 |
| |
| 気を付けておくことがもう一つあります。3つのうちの二つ、輻射率、伝達率は条件によって変わります。濃い色のコートのほうが、ホワイトのコートより暖かいですし、例えば、ピカピカに磨いた銀色の金属と、その金属に艶消しブラック塗料を塗った二つのサンプルに、電熱ヒーターを当てたら、艶消しブラック塗料を塗ったほうが温度が上がります。 |
| |
 |
| |
 |
| ● 製造現場の熱力学 |
| |
| 熱力学は、ある熱のつり合い(平衡状態)から次のつり合い状態になるとき、温度、圧力、体積のどれかを変えるとそのほかはどう変化するのかを明らかにする。正確には、原子(分子)の運動エネルギ―をある範囲の原子(分子)全部にわたって計算するのだと思うが、ここでは従来通りの方法、すなわち、ある領域をマクロ的に扱い、そこに有限要素法、古典的な微分方程式でつり合い方程式を適用する。 |
| |
| それぞれの意味するところなどは、流体力学、熱力学を参照してください。 |
| |
| 加熱炉、熱処理炉内の昇降熱時の速度の限界、鋼片、ビレット、板、パイプなどの均熱性、焼入れ性向上などを目的とした炉内温度分布制御ならびに冷却技術は、製造技術の重要な項目のひとつであるため、熱力学の基礎の理解は意義あることだと思われます。 |
| |
| ここでは、輻射(電磁気)、伝達(流体)、伝導を理解し、熱力学の3法則と、ニュートンの冷却則、フーリエの熱伝導方程式を紹介します。 |
| |
| なお、熱伝導率は、工具の焼き付きなど塑性加工とも関係があるという報告もありますが、ここでは割愛します。 |
| |
 |
| ● 基本的な量の定義 |
| |
 |
| ● 熱と温度 |
| |
| ー 熱 U |
| 物体に蓄えられたエネルギーの状態 |
| |
| ー 温度 T |
| 熱がどのくらい蓄えられたかあらわす尺度 |
| |
| ー 熱と温度の関係 (位置エネルギーと似ている。) |
| |
| U=mcT |
| U:熱エネルギー、m:質量、 c:比熱 c=ΔQ/ΔT (J/K)、T:絶対温度 |
| |
 |
| ● 最大温度と最小温度 |
| |
| 定義上温度には上限が無いが、高温では粒子がプラズマ化していて、どんどん温度を上げていくと粒子同士の相互作用でお互いが邪魔してそれ以上温度が上がらないポイントがあるような気もします。 |
| |
| 宇宙がビッグバンから冷え続けているなら、ビッグバンの温度が最高温度でしょう。ただし、相対性理論上ビッグバンからゼロ秒後は定義できないので、最も短い時間後(1プランク秒)の温度をプランク温度というそうです。これは約1.417×10^32 Kで、これより高い温度は無意味といわれています。 |
| |
| ちなみに、現在の宇宙の温度は3Kくらいで、プランク温度より低い理由は、宇宙が膨張しているからだと言われている。宇宙を膨張されるエネルギーがどこから来ているかは不明で、ダークマターではないかといわれているそうです。 |
| |
| 最低温度は、分子、原子の振動が止まる温度で、絶対零度といいます。 |
| |
| これ以上低い温度が無いのは、主に二通りの説明がされています。まず、状態方程式PV=nRTに従う理想気体では、温度ゼロで体積ゼロになり気体がなくなってしまいます。式で温度がマイナスだと体積もマイナスになるのでありえません。 |
| |
| 次に、電気抵抗値Rは温度を下げると低くなりますが、低温では、R=aT5+bT2+cT+R(R 不純物)で表され、不純物が無ければT=0でR=0になります。ちなみに、超伝導はこの式を検証中に発見されたそうです。 |
| |
| ただし、絶対零度より小さい温度についての論文もあるので、絶対零度が最小温度というのは正しくないのかもしれません。 |
| |
| 工業的に使う温度領域は、このうちのほんの狭い範囲なので、気にする必要もないといえばそれまでですが、調べていて「ほー」、っと思ったので書いてみました。 |
| |
 |
| ● 間違いやすい状態量の定義 |
| |
| ー 熱平衡: |
| 二つの物体を接触させ、十分時間がたって熱の移動がなくなった状態で、温度は等しい。 |
| |
| ー 熱源: |
| 他の物体と熱の授受があっても、温度が変わらない熱の供給源もしくは吸収源。 |
| |
| ー 状態量: |
| 熱平衡にある均質な物体の状態を表す物理量。 |
| 物質を分割しても変わらないものと、物質の量に比例して変わるものがある。 |
| 前者は温度T、圧力Pなど。 |
| 後者は体積V、内部エネルギーU、熱容量Q、エントロピーSなど。 |
| |
 |
| ● 温度の表記方法4つ |
| |
| 摂氏温度:真水が氷になる温度を0℃、沸騰点を100℃とし、その間を100分割したもの。 |
| |
| 華氏温度:真水が氷になる温度を32?、沸騰点を212?とし、その間を180分割したもの。摂氏温度との換算式は |
| F = 9/5 C + 32 |
| |
| 絶対温度:熱力学で使用する温度で、分子、原子の熱運動が完全に停止した状態を0°K(0K)、目盛間隔は摂氏温度と同じ。摂氏温度との換算式は |
| K = C + 273.15 |
| |
| プランク温度: 絶対零度から、ビッグバン直後の温度までを0から1にしたもの。相対性理論より計算できるということですが、割愛します。 |
| |
 |
| ● 熱輻射 Heat Radiation |
| |
| 赤外線などの電磁波が物質に作用して熱が伝わります。これは熱輻射によるものです。 |
| |
| 物質が周囲より温度が低い場合は物質は加熱され、逆に高い場合は物質は冷却されます。 |
| 炉壁から物質の表面への輻射、パイプ内表面内での輻射 |
| 熱が伝わると温度が変化するが、物質の比熱、質量により変化幅は変わる。 |
| |
| ● 輻射率 |
| 輻射によって放出するエネルギーと、同温度の黒体が放出するエネルギーの灯を輻射率(放射率)といいます。 |
| 0から1の間の数値となるが、同じ物質でも磨かれた金属表面や白色では小さく、黒い色ほど大きくなる。 |
| |
| 吸収率 |
| キルヒホッフの法則より、吸収率は輻射率と同じ値となる。 |
| |
 |
| ● 黒体、灰体、白体 |
| |
| 輻射で物体に入ってくるエネルギーは電磁波です。電磁波は、物体の表面で反射と吸収が同時に行われますが、反射した電磁波の波長が人間に見えると可視光といいます。(可視電磁波とはいわないですね。。)これが物体の色で、虹の色(赤、オレンジ、黄色、緑、青緑、青、紫)がその範囲です。可視光の外側がそれぞれ赤外線、紫外線といい、電磁波となります。 |
| |
| 外部から入ってくるあらゆる波長の電磁波(エネルギー)を吸収して反射しない物体が黒体です。黒体と反対に、あらゆる波長の電磁波を反射する物体が白体で、白体にはエネルギーが入りません。 |
| |
| 黒体と白体の中間が灰体で、反射と吸収の両方で物体とエネルギー交換をするので温度が変化します。 |
| |
 |
| ● キルヒホッフの法則 輻射エネルギーの吸収・反射 |
| |
| 輻射のシミュレーションを行う場合などで、輻射エネルギーの計算を行う場合の最初に考える項目として、ある点からの放射エネルギーはいくらで、対象物にどれだけ吸収されるかが重要になります。放射エネルギーは、ある点から直線で進めるどこにでも行け、入射エネルギーは、そのポイントから見えるところ全部から入ってくるので、放射する点全部を積分する必要があるが、ここでは、最初の一歩として、点と点を考えます。 |
| |
| 放射と吸収は、同じ「能」がつくので混同しやすいが、放射能は放射エネルギーで、吸収能は吸収される割合。吸収するエネルギー=放射能(入射)x吸収能。述語的に正しくないと思いますが、放射能は放射量、吸収能は吸収率と脳内変換するとわかりやすいかもしれません。 |
| |
| 放射能E 単位面積を単位時間に出る放射エネルギー(J/m2s)。 |
| 吸収能a 入射エネルギーのうち、吸収される割合。 |
| |
 |
| |
| 物体1の反射(放射)は、初項(1-a2)E1、公比 (1-a1)(1-a2)の無限等比級数になります。(上の絵で赤字の部分が初項と公比です。) |
| |
| 同じように考えて、物体1の吸収、放射、物体2の吸収、放射が計算できます。さらに、物体2の最初の放射E2もあるので、同様に計算できます。 |
| |
| 物体1放射は、物体1,2の放射の無限等比級数の和になります。無限等比級数の公式より、E1は次式で与えられます。 |
| E1 = a1(1-a2)E1 / ( (1-((1-a1)(1-a2)) ) + a1E2 / (( 1-((1-a1)(1-a2)) ) |
| = (a1E1 - a1a2E1 + a1E2) / (a1+a2-a1a2) |
| 両辺を変形すると、 |
| a1E1 + a2E1 -a1a2E1 = a1E1 - a1a2E2 + a1E2 |
| a2E1=a1E2 |
| E1/a1=E2/a2 |
| |
| 以上をまとめると、熱的な平衡状態で物体の温度が変わらないとすれば、物体の放射の総量Eは、二つの放射の和に等しい。この等式を変形していくと放射能と吸収能の比は一定となります。これを、キルヒホッフの法則といいます。 |
| |
 |
| ● 熱と絶対温度の関係 |
| |
| 熱はエネルギーで、黒体が放出するエネルギーは電磁波エネルギーです。熱(エネルギー)は、絶対温度の4乗に比例します。 |
| |
| ステファンボルツマンの法則 |
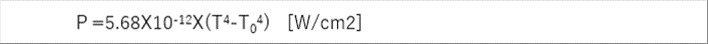 |
| P=5.68X10^(-12)X(T^4-T0^4) [W/cm2] |
| P>0 熱を放射 |
| P=0 熱を放射しない |
| P<0 入熱 |
| |
| 放射温度計は、赤外線強度を計測するのもが多いですが、紫外線を計測しても可能です。例えば、都市ガスを燃焼させて対象物を加熱する場合、都市ガス自体が対象物と同程度の赤外線を発するので、紫外線強度を計測して温度に換算する場合があります。 |
| |
 |
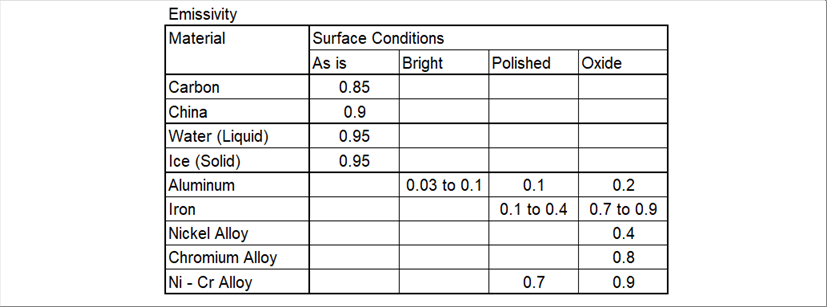
| ● 輻射率(放射率) |
| |
| おおよその数値は知られているが、物体の肌の様子、色などに影響される。物性値ではないので、状況応じて計測する必要があります。 |
| |
| 放射温度計の説明書には、対象物によって推奨値が書いてある場合が多いですが、合わないと感じた場合には、接触温度計と比較するなどが必要になります。 |
| |
 |
| |
 |
| ● 輻射率の測定 |
| |
| 計測時の安全上の配慮 |
| 計測対象からの熱輻射対策には防火服、熱気流対策にはフェイスガード、場合によっては呼吸器などが必要になります。また、計測時に転倒しても安全な場所から計測するか、転倒防止対策などを必要に応じて実施します。 |
| |
| 測定方法 |
| 接触式温度計との比較が一般的に利用されている。 |
| 接触温度計と同じ数値になるように放射温度計の放射率を変化させる。 |
| 計測時の誤差 |
| |
| 誤差の要因としては、測定領域の場所、広さの違い、太陽、隣のパイプなどの他の物体からの放射をひろう、水蒸気や湯気の影響などが考えられるので、測定する位置には十分注意する必要があります。また、誤差が大きいと感じられる場合には複数回の測定が必要になります。 |
| |
 |
| ● 熱伝達 Heat Transfer |
| |
 |
| |
| 上の絵は、焚火に丸い鍋をかけてお湯を沸かす様子を描いています。対象物は、焚火、丸鍋、水の3個なので、熱が伝わっているのは、焚火から鍋、鍋から水、水内部の3個に分けて考えるのがいいと思います。まず、焚火から鍋では、2つの現象が起きています。まず、焚火の炎の熱輻射が鍋に伝わっています。同時に、焚火の燃焼ガスと温まった空気の流れで鍋に熱が伝わっています。次に、鍋内部では熱が外側から内側に伝導し、鍋の内表面から水に熱が伝わっています。このため、水の炎に近い部分が最初に温まり、体積が膨張して軽くなり上に移動します。このように、流体(焚火の燃焼ガス、温まった空気、温まった水)が移動することとで物質に熱が伝わることを(自然)対流熱伝達といいます。 |
| |
| 熱伝達率は、流速、圧力、表面性状(粗さ、色など)によって変化します。このため、流体力学と密接な関係があります。 |
| |
| 詳細は、理論 熱伝達参照。 |
| |
 |
| ● 強制熱伝達率 |
| |
| 温泉などで、あまり熱さを感じなくなっても、湯をかき混ぜると熱く感じるのはかき混ぜて流れが生じたからと考えられます。 |
| |
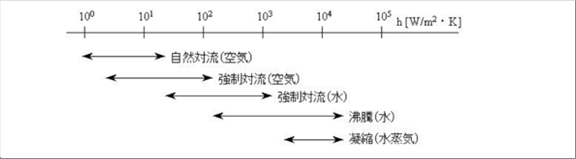
| 下の絵は、空気と水の状態で熱伝達係数がどのようになるかを示しています。おおむね自然対流(空気)>強制対流(空気)>強制対流(水)>沸騰水≒水蒸気の凝縮となっています。 |
| |
 |
| |
 |
| ● 熱伝導 Heat Conduction |
| |
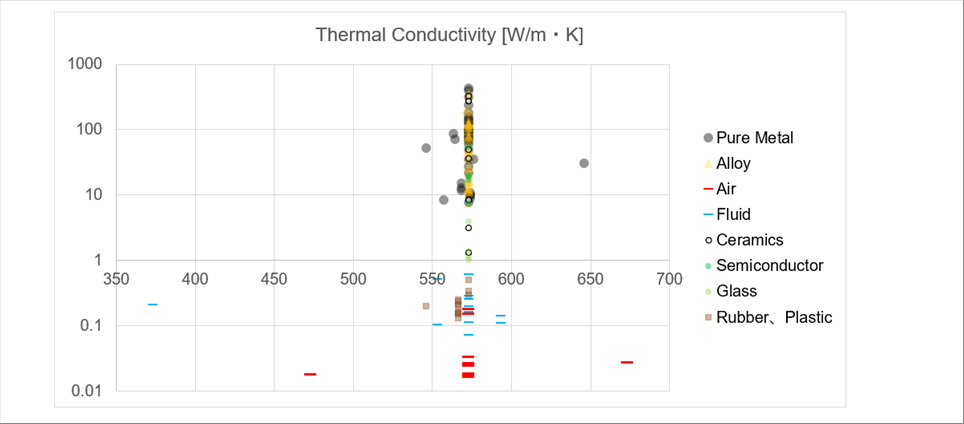
| 物質内部の原子(分子)運動が伝わることが熱伝導で、熱伝導率は物質によって一定値(物性値)となる。表面を黒くしても、ディンプル加工をしても熱伝導率は変化しない。 |
| |
 |
| |
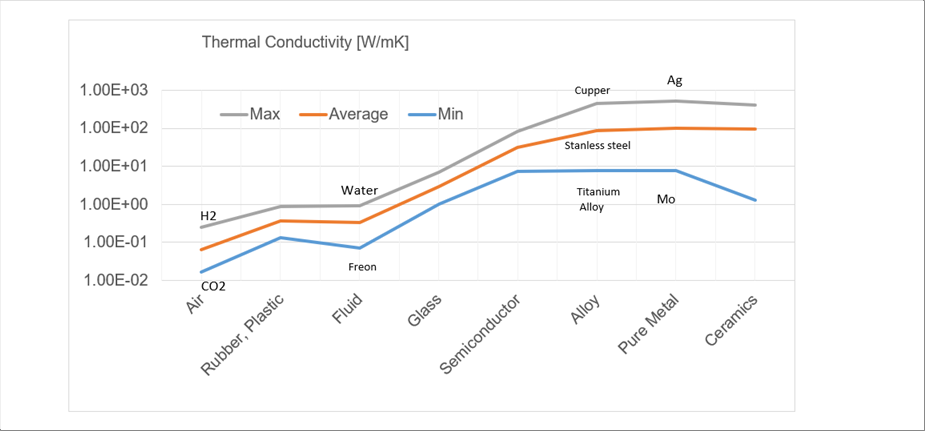
| おおむね、気体(耐火物)<液体<固体の順になっており、原子(分子)の振動が伝達されやすい順になっていると推測される。(水銀は常温では液体だが、除外した。) |
| |
| ばらつきの程度は、気体、液体では一桁以内の差だが、固体では、ゴム、プラスチックを入れると4桁のばらつきがある。 |
| |
| 合金:鋳鉄、S35C、工具鋼、マルテンサイト系/オーステナイト/フェライト系ステンレス、耐熱鋳鋼、インコロイ、ハステロイ、超超ジュラルミン、黄銅、クロム鋳鉄、ニクロム、超硬合金など。 |
| |
 |
| |
| 詳細は、理論 熱伝導参照。 |
| |
 |
| ● 熱力学 |
 |
| ● 気体の状態方程式 |
| |
| 理想気体の場合 PV= nRT |
 |
| 分子間の力、分子の大きさは無視。分子同士は衝突しない。壁との衝突は完全弾性。高温、低圧の気体には適用可能だが、実際の気体に適用すると誤差が大きい。 |
| |
| ● ファン・デル・ワールス気体 圧力、体積補正項がある。 |
 |
| a:圧力補正係数、n2/V2に比例。 |
| b:体積補正係数、nに比例。 |
| 実際の気体とは誤差がある。 |
| |
 |
| ● 熱力学の法則 |
| |
| ー 第一法則 エネルギー保存則 |
| |
| 吸収したエネルギーdQは、内部エネルギーの増加dUと外部にする仕事dWに等しい。 |
| 開放系では外部から物質が入ることによる変化量dZが加わる。 |
| 閉鎖系 dQ = dU + dW、開放系 dQ = dW + dU + dZ |
| |
| 注意:符号は言い方で変わるので、概念を一定にすること。 |
| 「物体に仕事Wと熱量Qを加えて状態AからBに変化させたときに内部エネルギーが変化するdU。」 |
| 閉鎖系 dU = dW + dQ |
| 重要: dQ, dWは単に微小な量という意味。これらは状態量ではないので、微分ではありません。 |
| |
| ー 第二法則 |
| |
| 熱エネルギーは高温部から低温部へ移動し、その際に仕事をする。逆は起こらない。かつ、熱を全部移動させることはできない。 |
| 永久機関は実現不可能。 |
| |
| 断熱系では、エントロピーS(次ページ)は増大する。 |
| |
| ー 第三法則 |
| |
| 絶対零度近辺では、温度が絶対零度に近づくに従い、エントロピーはゼロになる。 |
| |
 |
| ● ニュートンの冷却の法則 |
| |
| 大気中で何かを放冷するなど、熱いものほど早く冷め、大気温度に近くなるとなかなか冷え切らない。実験で、温度と時間を計り、この温度差と熱の移動量が比例することがわかっている。 |
| |
| ー ニュートンの法則 |
| |
| 「媒質中に置かれた物体の熱量Qの時間的変化量は、物体の表面積S、ならびに、媒質の温度Tmとその媒質中に置かれた物体の温度Tの差に比例する。」 |
| |
| この比例定数を熱伝達率hという。 |
| |
| 物体の熱容量C、表面積 s、冷却開始時の物体の温度T0として、微分方程式を解く。物体に出入りした熱量ΔQも求められる。微分方程式を省略して解だけ書くと、時刻tにおける温度Tは次式で与えられる。 |
| |
| T = (T0-Tm) exp ( - hst/C ) + Tm |
| ΔQ = C(T-Tm) |
| T0: 冷却開始時の物体の温度、s:表面積、h:熱伝達係数、Tm:媒質の温度(周囲の温度) |
| |
 |
| ● 冷却時の温度予測 |
| |
| どのくらいの時間で何度まで冷却できるかの計算をニュートンの冷却則で予測する。 |
| |
| 既知数と未知数 |
| |
| 既知数は、物体の初期温度To, 大気温度もしくは水温Tm, 物体の表面積S。実際は変動するが、変動幅が小さいか、小さく制御できるので既知数と言える。 |
| |
| 媒質の温度(一般的な製造現場では、大気温か冷却水温)は季節で変わるので注意が必要な場合がある。 |
| |
| 未知数は熱伝達率hと熱容量Cの二つなので、2回計測すれば特定できる。 |
| |
| 安全上の問題などで時刻と温度が正確に測れない場合は、3回以上計測して複数データを採取すると誤差を小さくできる。 |
| |
 |
| ● 熱伝達と温度境界層 |
| |
| 固定平板の上の流れの概略は、流体力学を参照してください。層流の流体の流れは中央が最大で、壁面では相対速度がゼロになります。温度はそれと違い、物体表面で物体と同じ温度、物体から離れるに従い、徐々に変化して十分離れた位置で一定値(流体の設定温度)になります。この、流体の温度が変化する領域を温度境界層といいます。 |
| |
 |
| ● 熱伝導方程式, フーリエの法則 |
| |
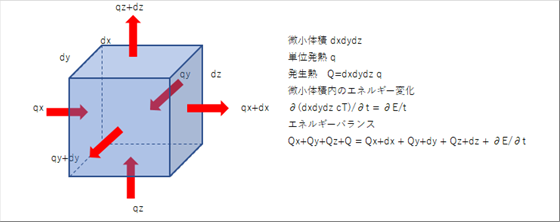
| 熱輻射と熱伝達で、物体の表面に熱エネルギーが入ると、物体の温度が時間と物体内の位置で変化していく。この、物体内の温度の分布を式にしたものが熱伝導方程式と呼ばれる。 |
| |
 |
| |
| 微小体積dxdydzのエネルギーバランスの式から、熱伝導方程式が導かれます。詳細はシミュレーションを参照してください。 |
| |
| Author: T. Oda |
| このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。 |