Thermodynamics Basics
(1) How Heat is Transferred.
(2) Thermodynamics in the manufacturing floors
(3) Definitions of the Basic Values
(3)-1 Heat and Temperature
(3)-2 Maximum and Minimum Temperatures
(3)-3 Definitions that are easy to make Mistakes
(3)-4 Four (4) Units of Temperature
(3)-5 Heat Radiation
3-(5)-1 Emissivity and Absorption Rate
3-(5)-2 Black Body, Gray Body, White Body
3-(5)-3 Kirchhoff's Law, Calculation of Reflection and Absorption of Radiation
3-(5)-4 Stefan Boltzmann's Law, Relation between Heat (Energy) and Temperature
3-(5)-5 Emissivity
3-(5)-6 Measuring Emissivity
3-(6) Convection Heat Transfer
3-(6)-1 Forced Convection Heat Transfer
3-(7) Heat Conduction
3-(8) Thermodynamics
3-(8)-1 Equation of State, Gas
3-(8)-2 Three Laws of Thermodynamics
3-(8)-3 Newton's Law of Cooling
3-(8)-4 Temperature Calculation during Cooling
3-(8)-5 Convection Heat Transfer Coefficient and Velocity Boundary Layer
3-(8)-6 Fourie's Law of Thermal Conduction
(1) How Heat is Transferred.
The heat transfers from the hotter object to the cooler ones. The direction of the transfer does not change. There are three (3) ways of the transfer, which are the radiation, the convection, and the conduction. The 3 words are free to use in the usual life, or simply "heat transfer". However, it is desirable to understand the differences clearly in the industry. In many cases, the 3 ways of transfer occur at the same time. The following picture illustrated the 3 ways.
Fist of all, the heat is the energy. Therefore, it is easy to understand the transfer of heat is that of energy.
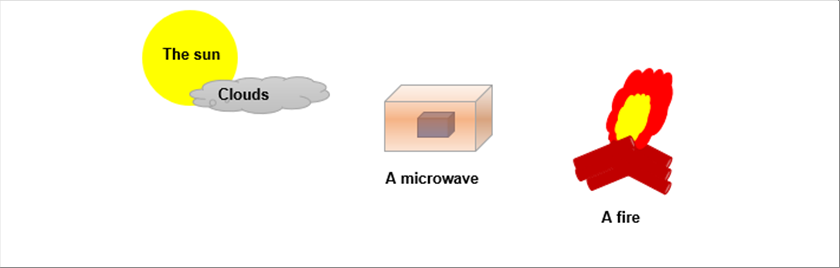It is wan under the sun, but it becomes cooler when it is cloudy. We can use a microwave to heat a food. We feel warm even we are sitting at bit far from the camp bonfire. The reason why the sun is warm is because the heat energy transfer in the vacuum space and in the air. The reason why the bonfire is warm even when we sit upwind is because the heat transfers in the air. If we sit downwind, we feel warmer, because the warn air also comes to us. The reason why it is cooler under the cloud is because the cloud, which is made of water and vapor, absorb the heat energy before it comes to us. These are called "heat radiation".
The above picture shows the temperature distribution of a cold object on a hot plate. The cold object receives the heat radiation from the hot plate and the warm air at the same time. Because the hot air moves upward. The temperature of the bottom of the object rises and then the rest becomes hot gradually. The bottom surface receives both of the radiation and the rising hot air. The other side surfaces receive both of them but less than the bottom surface. The inside of the object receives none of them but the temperature also rises because it receives heat from the surfaces.
As seen in the picture, there are three (3) ways of heat energy transfer, which are the energy radiation from the hot plate, the convection of fluid (air), and the conduction inside of the object. The 3 happen at the same time.
Another important thing is that the two (2) of them, which are the heat radiation and the convection change due to the conditions. For example, the color does affect the performance, the black object becomes hot faster than the white one does. Another example, the surface roughness does affect either, the object with rough surfaces become hot faster than that with the mirror like ones. On the contrary, the heat conduction inside of the object does not change by the conditions for a material.
(2) Thermodynamics in the manufacturing floors
The thermodynamics clarifies the new values of the temperature, the pressure and the volume when an equilibrium state changes from one to another. In the today's technology, each movement of each molecule or atom can be calculated; however, in the page, let's follow the conventional method. We analyze the area by the equilibrium equations in the differential equations. The finite element method is often utilized for the analysis.
Please see the flow dynamics and thermodynamics for detail.
The productivity and uniformity of the materials in the heating and heat treatment furnaces are one of the main targets of the manufacturing technology. The main products may be plates, sheets, and pipes. Understanding of the basis of thermodynamic may help improvement quenching ability as well.
Therefore, we see the basis of radiation, convection, and conduction of heat. The law of thermodynamics and the newton's law of cooling and the Fourie's law of thermal conduction are introduced.
It is said that the heat conductivity is connected to the sticking of tools for the metal plastic deformation; however, let me skip it.
(3) Definitions of the Basic Values
(3)-1 Heat and Temperature
- Heat U
The heat is the state of energy that is stored in a material.
- Temperature T
It is the index, which indicates how much of the heat is stored.
Relationship between heat and temperature (It is like the potential energy.)
U = m c T
U: Heat enery, m: mass, c: specific heat, c=��Q/��T (J/K), whre T: absolute temperature
(3)-2 Maximum and Minimum Temperatures
There is no upper limit in the temperature by definition; however, there might be the upper limit, above which is useless to consider.
It is said that the space has been reducing the temperature since the Big Bang. If it is true, the maximum temperature should be that of the Big Bang. However, according to the theory of relativity, the temperature of zero (0) second after the Big Bang cannot be defined. The minimum time is said one (1) Plank time second. The Plank temperature is defined that the temperature after 1 Plank time second after the Big Bang. It is about 1.417�~10^32 degrees K, and they say that the temperature higher than that is meaningless.
Just in case, the current tempearture of the space is about three (3) degrees K. The reason why it is smaller than that of the Plank temperature is because the spece has been expanding. It is unknown where the energy that expands the space comes from. They say that it is due to the black matter.
The minimum temperature is defined that the oscilation of atom stops. It is the absolute zero (0) degree.
There are two (2) explanations why it is the minim temperature. Firstly, the volume V of the ideal gas, which follows the state formula PV=nRT, is zero (0) when the temperature T is zero (0). If the temperature is minus value, the volume is also minus value, which does not make sense.
Another explanation is as follows. The electric resistance R becomes smaller as the temperature decreases. In the very low temperature, the R is defined as R=aT5+bT2+cT+R�iR* impurities). If there is no impurities, R=0 at T=0. If the temperature T is negative, the resistance is negative, which does not make sense neither. Just in case, the superconductivity was found during the evaluation process of the formula.
I found an article in the web that tells the author of the article found the temperature less than the absolute zero (0). If so, the minimum temperature might be below the absolute zero (o) degree.
Anyway, the temperature range for the industry is very limited one, such as from one hundred (100) degrees K to one thousand eight hundred (1 800) degrees K.
(3)-3 Definitions that are easy to make Mistakes
- Thermal equilibrium
A material contacts another, After a long time, the heat exchange between the materials stops The temperatures of both materials are same.
- Thermal source
The source of heat, whose temperature does not vary even after the heat exchange with the other material(s). It is either the heat supply or heat absorption sources.
- State Quantity
The physical values that show the state of a homogeneous material in the thermal equilibrium.
There are two (2) kinds of the values. One is what is unchanged after division of the material. Another is what varies according to the quantity of the material.
Unchanged ones: Temperature T, Pressure P
Variable ones: Volume V, Internal energy U, Thermal capacity Q, Entropy S.
(3)-4 Four (4) Units of Temperature
Celsius Temperature C: Temperature for pure water to turn into ice is zero(0) degree, boiling point is one hundred (100) degrees. Divide the range from 0 to 100 into 100 equal parts.
Fahrenheit Temperature F : Temperature for pure water to turn into ice is thirty two (32) degrees., the boiling point two hundred twelve (212) degrees. Divide the range from 32 to 212 into 180 equal parts.
F = 9/5 C + 32
Absolut Temperature K: Temperature for molecules and atoms to fully stop is zero (0) degree, the scale interval is same as that of Celsius temperature.
K = C + 273.15
Plank Temperature: It is from 0 K to the very high temperature, which is after the Big Bang. The range is from zero (0) to one (1). It is possible to calculate by the theory of relativity, but please let me skip it.
(3)-5 Heat Radiation
The heat (energy) transfers by the action of the electromagnetic waves such as infrared ray. It is called the heat radiation.
A material is heated when the temperature of the material is lower (cooler) than the surrounding area. On the contrary, it is cooled down when the temperature is higher (hotter).
For example, the heat radiation between the surfaces of the walls of the furnaces and the material is always happening, because there are different temperatures. Another example is what is inside of a pipe. The temperature differences among the inside surface of a pipe is usually smaller than that of the first example, though.
The temperatures of both materials change when the heat transfers. The magnitude of the change is affected by the specific heat, the mass, and so on.
3-(5)-1 Emissivity and Absorption Rate
The emissivity is defined as the ratio between the emitted energy of the material and one of the blackbody of the same temperature.
The emissivity is between zero (0) and one (1). It varies in a same material. It is smaller when the surface is polished or white color, and is bigger when it is black.
By the Kirchhoff's Law, the absorption rate is same as the emissivity.
3-(5)-2 Black Body, Gray Body, White Body
The energy that enters into a material by the radiation is the electromagnetic wave. It reflects on the surface of the material and the rest enters into the material. Both of the reflection and the absorption occur at the same time. We can see some of the reflected electromagnetic wave. It is called the visible light. (One note is that it is not called the visible electromagnetic wave.) The visible lights are the colors of materials. The seven (7) colors of the rainbow are red, orange, yellow, green, blue, indigo, and violet. The next to the red is the infrared ray, and purple is ultraviolet ray, both of which are the electromagnetic waves.
The Black body absorbs every wave length of the external electro magnetic waves, including the visible lights, and reflects nothing. On the contrary, the white body reflects all of them, and no energy transfers into the white body.
The gray body is between the black and the white bodies. It exchanges energy with the other materials by reflection and absorption of energy. Therefore, both of the temperatures of the gray body and the surrounding materials change.
3-(5)-3 Kirchhoff's Law, Calculation of Reflection and Absorption of Radiation
One of the first item of the temperature simulation may be the calculation of the absorption of the emitted energy from a source. The emitted energy moves straight to anywhere. And, an absorption point receives every energy as long as the point can "see". Mathematically speaking, it is an integral of all "visible" areas. To start with, let's begin two (2) points, one emits and another absorbs.
The following picture shows a trace line of one (1) ray, which the material 1 emits.
Unit emission energy: Emission energy that a unit surface emits in a unit time (J/m2s).
Absorption energy: absorption rate a times unit emission energy.
The reflection of the material 1 is the infinite geometric series of the initial item is (1-a2)E1 and the common ratio (1-a1)(1-a2). They are indicated in red in the above picture.
The absorption of the material 1, emission and absorption of the material 2 are considered same as above.
The emission of the material 1 is the addtion of the infinite geometric series of the materials 1 and 2. By the formula of the infinite geometric series, E1 is dedined as follows.
E1 = a1(1-a2)E1 / ( (1-((1-a1)(1-a2)) ) + a1E2 / (( 1-((1-a1)(1-a2)) )
= (a1E1 - a1a2E1 + a1E2) / (a1+a2-a1a2)
And then, let's change the both sides of the equaition as follows.
a1E1 + a2E1 -a1a2E1 = a1E1 - a1a2E2 + a1E2
a2E1=a1E2
E1/a1=E2/a2
We got the two (2) important facts in the formulas. The second line of E1 says that under the condition of the thermal equilibrium, the temperature of the materials do not change, the total emission E is equal to the two (2) emissions. Another is that the ratio E/a is constant. This is the Kirchhoff's Law.
3-(5)-4 Stefan Boltzmann's Law, Relation between Heat (Energy) and Temperature
Heat is energy. The energy emitted from the black body is electromagnetic one. Heat is proportional to the fourth power of absolute temperature.
Stefan Boltzmann's Law
�o=5.68X10^(-12)X(T^4-T0^4) [W/cm2]
P>0 It emits heat.
P=0 No emission.
P<0 It absorbs heat.
Many radiation thermometers measure the infrared intensity. It is also ok to measure the intensity of the ultraviolet. For example, if the fuel is the natural gas for the heating of the steel material, both of the natural gas and the steel generate the similar quantity of the infrared ray, it is necessary to measure the ultraviolet for the temperature.
3-(5)-5 Emissivity
The rough number is know for each material; however, it varies due to surface consitions, such as color and roughness. Therefore, it is suggested to measue for the material to be measured.
The known numbers are usually shown on the instruction manual of the thermometers. If the measured temperature is questionable, please measure the temperature with a contact thermometer, for example. Then, you can guess the suitable number for the case.
3-(5)-6 Measuring Emissivity
Pay attention to Safety
It may be necessary to prepare a fire protection clothing, a face guard, and a restiratory system, depending on the measuring condition. Please also pay attention to the measureing place, because you may fall during measuring. It may be necessary to prevent the fall.
Measuring emissibity
It is commonly adopted to compare the contact and the radiation thermometers.
it is to change the emissivity up to the value when the two (2) measuring values match.
Possible causes of errors
It is known that the emissivity changes when the temperature changes, therefore, it is advisable to pay attention to the temperature of measuring. As seen in the above table, the surface condition is another cause, it is necessary to use the material with the same surface condition. The vapor absorbs the radiation, the reflection of the sun or lights, and the measuring angle can also be the causes. Therefore, it is advisable to find the suitable place for the measurement, and you may need to measure some times to minimize the deviations.
3-(6) Convection Heat Transfer
The above picture shows how the water in a round pot is boiled on the bonfire. There are three (3) objects, which are the bonfire, a round pot, and the water inside. The heat transfers from the bonfire to the pot, then from the pot to the water. Let's consider the condition in the two (2) parts. Firstly, the heat radiation of bonfire is transferred to the pot. At the same time, both of the combustion gas and the warmed air move to the pot and the heat is also transferred to the pot. And then, inside of the pot, the heat is transferred from the outside surface to the inside surface. The inside surface transfers the heat to the water. Therefore, the water, which is closer to the bonfire, becomes warm earlier than the rest. The heated water expands and it becomes lighter. Therefore, the heated water moves upward. As seen here, the heat transfer due to the movement of liquid (the combustion gas, warm air, and heated water) is called the (natural) convection heat transfer.
The convection heat transfer coefficients varies due to the velocity, the pressure, and the surface conditions (such as color and roughness) of the liquid. Therefore, it is strongly connected to the fluid mechanics
Please see the theory of the convection heat transfer for detail.
3-(6)-1 Forced Convection Heat Transfer
After you do not feel the temperature in the hot springs, you feel it again when you stir the hot water. It is due to the generation of flow by the stirring.
�@The following picture shows the ranges of the heat transferring coefficients of the several conditions of air and water. The order is natural convection (air) > forced convection (air) > forced convection (water)> boiled water > condensation (vapor).
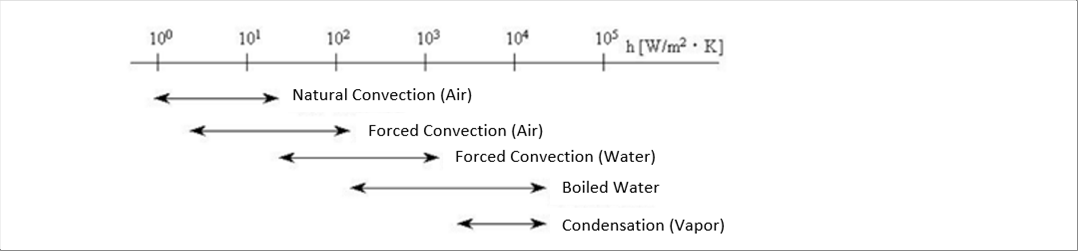3-(7) Heat Conduction
The heat conduction is the transferring of the atomic (or molecular) motions of the material. The coefficient of the heat conduction is constant for each material. The surface conditions, such as color and roughness, does not affect the coefficient.
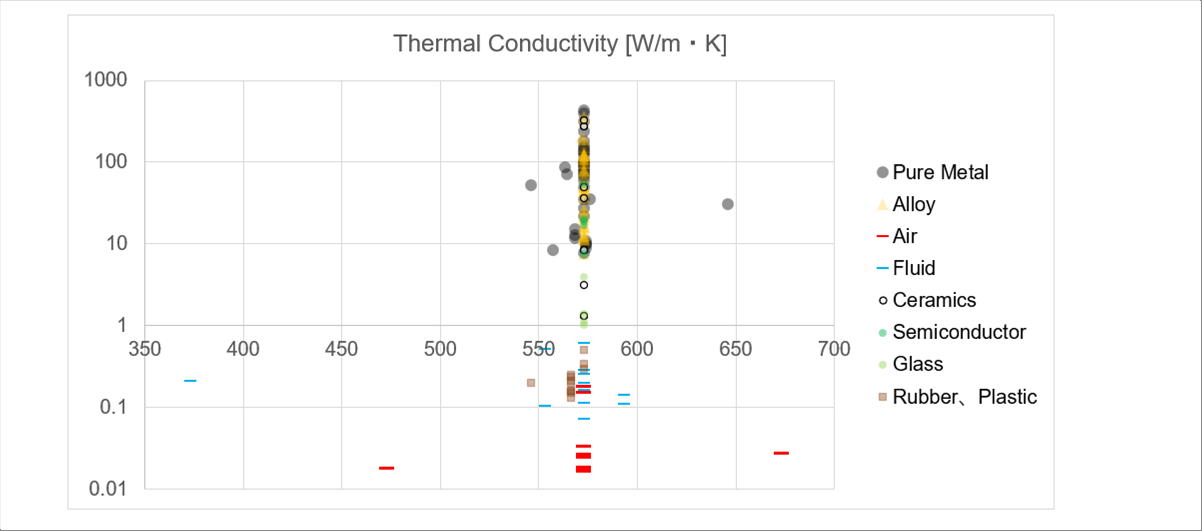It is roughly air < fluid < solid. The order of the thermal conductivity looks that of the density. The higher the density, the easier in transmitting the atomic (or molecular) vibrations. (Mercury, which is liquid matal, is omitted.)
The variation of air and fluid are smaller than that of the solid.
Alloys: Cast iron, carbon steel, brass, tool steel, stainless steel, heat resistant steel, incoloy, hastelloy, super super duralumine, chrome cast iron, cemented carbide.
Please see the theory of the heat conduction for detail.
3-(8) Thermodynamics
3-(8)-1 Equation of State, Gas
The equation of state, ideal gas; PV= nRT
Both of the force among and the size of the molecules are omitted. No collision of molecules, perfect elasticity of collision between the wall and the molecules are also considered. Therefore, it is applicable to the high temperature and low pressure ones. There will be errors for the application of the actual gases.
Van der Waals equation introduces the correction terms of the pressure and the volume.
a: Pressure correction term, which is proportional to n^2/V^2.
b: Volume correction term, which is proportional to n.
The actual gases do not perfectly follow the above equation.
3-(8)-2 Three Laws of Thermodynamics
Fisrt law of thermodynamics
The absorbed or released energy dQ is equal to the change (increase or decrees) of the internal energy dU and the work toward outside dW.
isolated system, dQ = dU + dW
Open system, the change of the mass dZ is added.
dQ = dW + dU + dZ
NOTE: It is necessary to keep the steady concept in order to make sure the correct plus and minus signs
For example, the following concept is also ok. "When the state of a material is changed from A to B by the additional work dW and energy dQ. The internal energy changes, dU." The equation of the closed system is as follows. It is different from the above one.
Isolated system: dU = dW + dQ
Important: dQ, dW, dU simply mean small quantity. It is not the state quantity, and therefore, it is not the derivative.
Second law of thermodynamics
Heat energy always moves from hot areas to cold areas. There is no reverse movement. Work is done during the movement. It is impossible to transfer whole heat.
A perpetual motion machine is impossible.
The state of the entropy S always increases in the isolated system.
Third law of thermodynamics
When temperature is near absolute zero , entropy is zero as the temperature becomes close to absolute zero.
3-(8)-3 Newton's Law of Cooling
If a hot material is left in the air, the hotter the material, the faster it cools down. If the temperature is near the air temperature, it cools down very slowly. It is known by experiment that the amount of heat transferred is proportional to the temperature difference.
Newton's law of cooling
"The change of the heat quantity Q of a body in the medium is proportional to the surface area S and to the difference of the temperatures between the media Tm and the body T." The media can be the environment.
The coefficient of the proportion is the heat transfer coefficient h.
Heat capacity of a body �b, temperature of the body before the cooling T0, surface s, . The temperarure at time t and the heat capacity into/out of the material is obtained as follow. (Let me skip the differential equation.)
T = (T0-Tm) exp ( - hst/C ) + Tm
��Q = C(T-Tm)
T0: Temperature of the body before cooling, s: surface area, h: coefficient of convection heat transfer, Tm: Temperature of the media (environment)
3-(8)-4 Temperature Calculation during Cooling
Let's calculate the temperature during cooling.
Known and unknown values
The known variables are the temperature of the body before cooling To, temperature of media, which is usualy air of water Tm, and surface area of the body S.
The temperature of the media, which is usually air or colling water, may change according to the seasons.
There are two (2) unknown variables, which are the convection heat transfer coefficient h, and the heat capacity C. Therefore, if we measure two (2) times, we can define both of them.
Due to the safety reasons, for example, if time and temperature are not accurate, three (3) or more times of measurement may help to minimize the deviation.
3-(8)-5 Convection Heat Transfer Coefficient and Thermal Boundary Layer
Please see the fluid dynamics for the flow on the fixed plate. The speed of the laminar flow between the plates is maximum at the middle of the plates. The relative speed on the wall is zero (0). Different from the velocity variation, the temperature on the wall is same as that of the wall, and it reduces as the distance from the wall increase. And it becomes constant when the distance is big enough. The constant is the temperature of the set temperature of the fluid. The layer where the temperature varies is called the temperature boundary layer.
3-(8)-6 Fourie's Law of Thermal Conduction
The heat energy enters to the material on the surface by both of radiation and convection. And then, the temperature of the material start changing by time and positions. The equation to express the temperature distribution inside of the body by time is the Fourie's law.
The above picture shows the energy equilibrium of a tiny volume dx dy dz. It leads to the equation. Please see the temperature simulation for detail.
Author: T. Oda
The page was prepared in Excel, and html and css files were automatically generated by the excel2web.