| |
 |
| |
 |
| ● 計算条件 |
| 加熱炉の形状、材質 |
| ● シミュレーションに使う方程式 |
| 差分方程式の内容 |
| プログラムを組む場合の補足 |
| エクセルのワークシートで計算する場合の補足 |
| ● 計算結果 |
| エクセルのワークシート |
| エクセル 3D等高線図 |
| 回転行列 3D回転グラフ |
| |
 |
| ● 計算条件 |
| |
 |
| ー 加熱炉の形状、材質 |
| |
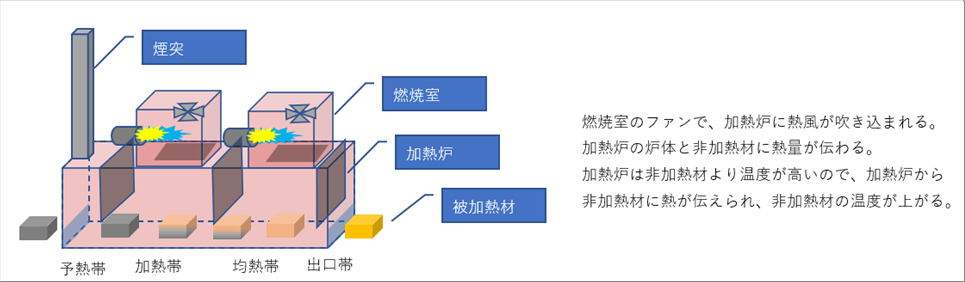
| 加熱炉の内面をどこまでシミュレーションするかですが、全部の形状、材質を図面通りにすることもできるし、天井と床は平行平板(もしくは円板)と仮定することもできます。 |
| |
 |
| |
| 上の炉の絵はエクセルの図形だけで作った単純なものですが、これでも全部をシミュレーションする場合には相当な手間がかかると思われます。 |
| |
| ここでは、シミュレーションを単純にするために、炉の形状は無視して、丸鋼片の外周の温度が決まっている場合をシミュレートしてみたいと思います。 |
| |
 |
| ● シミュレーションに使う方程式 |
| |
| 外周温度が与えられる場合は、熱の伝わりの3要素、熱輻射、熱伝達、熱伝導のうち、熱伝導のみとなります。熱伝導の微分方程式は、特別な場合を除き解析的に解けないので、差分法をもちいて丸鋼片の内部温度の計算をします。(もちろん、差分法以外の数値計算法でもかまいません。) |
| |
| 丸鋼片の内部温度計算なので、極座標を用いて計算してみたいと思います。極座標の差分法の方程式は、次の式となります。 |
| |
 |
| |
 |
| ー 差分方程式の内容 |
| |
| 式の詳細は、理論 熱伝導を参照してください。円柱座標では、中心部が点になるので、中心部のほかの解析(ひずみなど)をしたい場合は、直交座標系のほうが適しているかもしれません。シミュレーションの目的にあった座標系を使ってください。 |
| |
| Tが温度で、r、θが極座標での位置です。Tの右肩のnは、n回目、n+1がその次です。Tの右足のi, jは、極座標での順番になります。 |
| |
| 初期条件をn=1とすると、n=2が、⊿t 0.001 秒後の温度です。10秒後のn=10000が最終となります。 i,j は、1から分割数までです。 |
| |
 |
| ー プログラムを組む場合の補足 |
| |
| プログラムを組む場合は、VBAなどはi,jはゼロからでもエラーになりませんので、0から計算しても差し支えありません。 |
| |
 |
| ー エクセルのワークシートで計算する場合の補足 |
| |
| エクセルの表で計算する場合は、セルの縦と横にrとθをとり、あるセルに接している4セルの値で計算できます。エクセルの表で途中経過を保存する場合は、ほしい時刻で繰り返し計算を止めて、別表に書き出しておくといいです。 |
| |
 |
| ● 初期条件 |
| |
| 長い丸鋼片の中央部の昇熱を計算しますが、初期条件としては、下記とします。 |
| 時間差分: 0.001 sec |
| 半径:85mm、分割数=20 |
| 角度:0-2π、分割数=21 |
| 初期丸鋼片温度: 300度K |
| 丸鋼片外周温度:1000度K |
| 炉庄温度 : 800度K |
| 極座標(r、θ)なので、外周温度は、r=85mm、炉庄温度は、外周部円周2分割分とします。 |
| |
 |
| ● 温度ミュレーション方法 |
| |
| 差分の式と初期条件をプログラムを組むか、エクセルのワークシートに展開して計算します。必要な時間分繰り返し計算をします。例では、⊿t=0.001秒としたので、10秒の計算では、1万回の計算が必要になります。 |
| |
| 計算結果だのみの出力でもいいですが、3秒後、5秒後など、途中経過を出力すると、例えば中心部での昇熱カーブが得られます。 |
| |
| 計算に使ったラップトップのスペックは、corei5 4コア RAM 16GBです。繰り返し回数は1万回でしたが、ほぼ瞬時に終わりました。 |
| |
 |
| ● 計算結果 |
| |
 |
| ー エクセルワークシート |
| |
| 10秒後の計算結果は下の表となりました。 |
| |
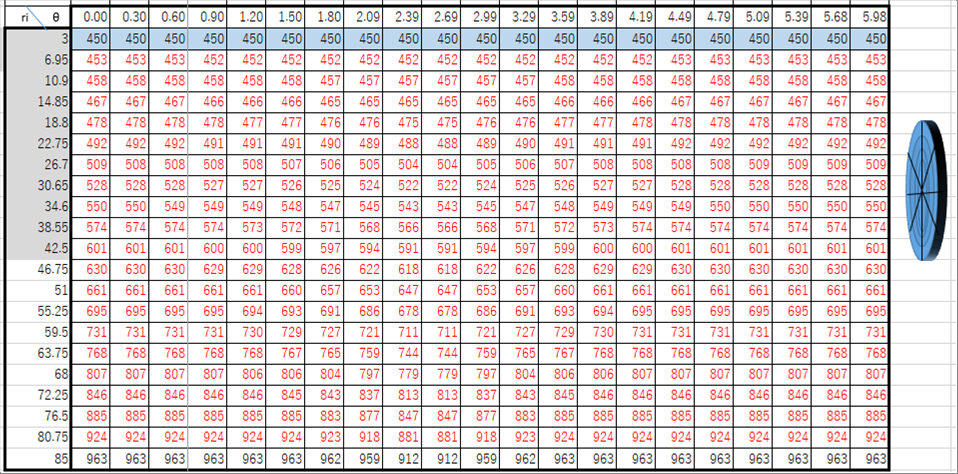 |
| |
 |
| ー エクセル 計算結果のグラフ表示 |
| |
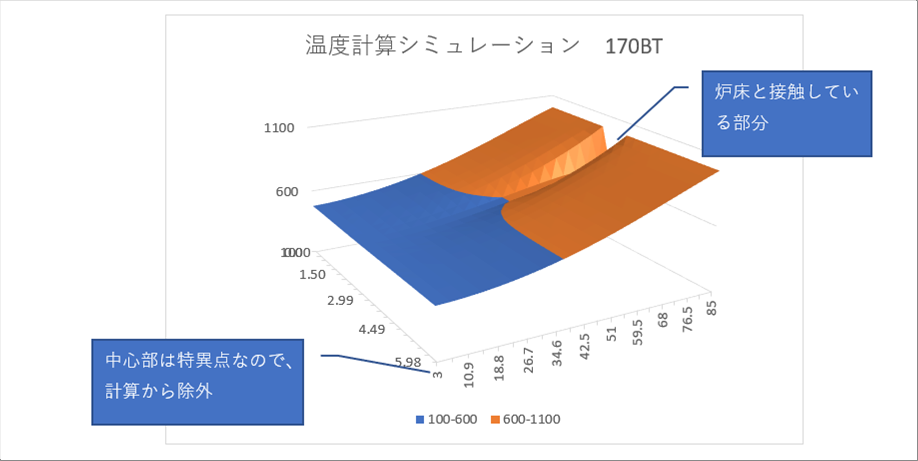
| 座標データは2Dですが、温度を入れると3Dになるので、エクセルの3D等高線図を使いました。エクセルには、極座標用のいい3Dグラフが見つからなかったので、等高線図で結果を表示すると、次のようになります。 |
| |
 |
| |
| 外周(r=85mm)の中央あたりが凹んで見えますが、鋼片が炉床と接触しているとして温度を下げた部分です。 |
| |
| |
 |
| ー 回転行列 3Dグラフ |
| |
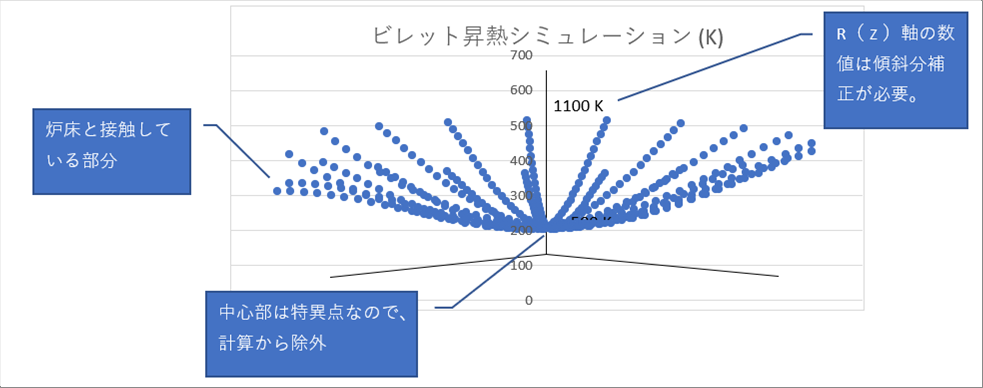
| 3D回転で紹介した方法で、回転行列を利用してr、θ、tの3Dのデータを、R(x),R(y)、R(z)に変換して、そのうちのR(x)とR(z)のデータで散布図を描いたものです。(詳細は「3D回転」を参照してください。) |
| |
| R(x)軸で64度回転、R(z)軸でー43度したものです。 |
| |
 |
| |
| 回転行列で3Dデータを2Dに変換しているので、散布図の軸は非表示、温度計算結果のデータに軸のデータを追加して、軸もデータと一緒に回転させています。 |
| |
| R(z)軸も若干手前に傾いているので、エクセルの縦軸の数字は正確ではありません。R(z)軸の傾斜分を補正して温度の数値を入れるのが正解ですが、イメージがわかればいいと思いましたので、散布図の縦軸をそのまま表示しています。 |
| |
| 丸鋼片が炉床と接触する部分は左側に来ています。 |
| |
| |
| |
| |
| |
| Author: T. Oda |
| このページは、excel2webで自動作成しました。 |
| |
| |
| |
| |