Temperature Simulation
(1) Calculation Conditions
Shape and Materials of the Heating Furnace
(2) Equations of the simulation
(2)-1 Difference Equations
(2)-2 Nots for the Programming
(2)-3 Notes for the Functions in the Spreadsheet
(3) Initial Conditions
(4) Temperature Simulation
(5) Outcome
(5)-1 Spreadsheet, Excel
(5)-2 Add-in 3D graph, Excel
(5)-3 Rotation Matrix, 3D Graph
(1) Calculation Conditions
Shape and Materials of the Heating Furnace
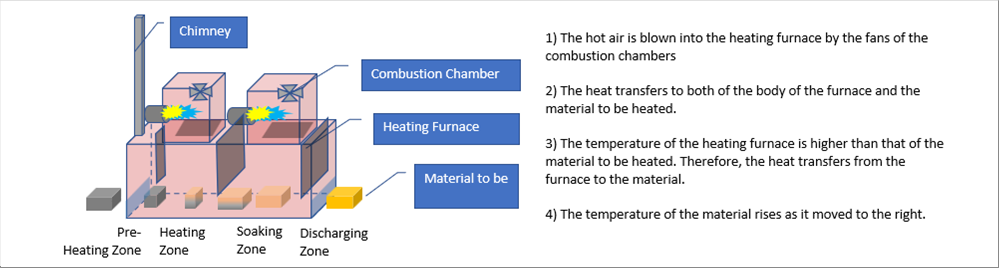
The following picture shows a heating furnace. The question is what are the necessary items for the temperature calculation. The material to be heated is a must. We should define which parts of the heating furnace to adopt to the calculation. We can use only the roof and the floor, which may be assumed as plates. Or, we can use the drawings for the full simulation, but it may be too much.
There are two (2) combustion chambers on the top of the furnace. The simulation may start from the gas fuel combustion. It may take a big effort. We may be able to find the better condition to meet the objective of the calculation.
In order to simplify the conditions, let's ignore the detail shape of the furnace. Let's assume that the temperature of the outside surface of the round billet are defined and calculate the temperature distribution inside of the billet.
(2) Equations of the simulation
If the temperature of the outside surface of the billet are known, we only consider the heat conduction, and we can forget the radiation and the convection of the heat. Because the two (2) items are to define the temperature of the outside surface. The differential equations of the heat conduction cannot be solved except very special case. We utilize the difference method for the calculation. (Other approximate methods are also ok.)
We use the cylindrical coordination system for the calculation of the round billet. The difference equation of the heat conduction is as follows.
(2)-1 Difference Equations
Please see the theory of the heat conduction for detail. The center of the circle is a singular point. Therefore, the calculation starts bit far from the center. Please use the adequate coordination system to meet the objectives of the simulation. It may be necessary to use the rectangular coordinate system for the calculation, or, small oval shape may be suitable for the cylindrical one.
T stands for Temperature. The n of the right top corner of T means the n-th times, and n+1 means the next one. The footers i and j means the orders in the coordination.
Let's assume the initial state as n=1, and delta t is 0.001 second. The next value can be calculated by the formula. We can continue the calculation until the time t reaches the desirable time. If we calculate the temperature distribution of 10 seconds later, n=1000. It means, we will get the solution after one thousand times of repetition.
(2)-2 Nots for the Programming
The number zero (0) is ok for the starting number in VBA. So, we can count i and j from zero (0).
(2)-3 Notes for the Functions in the Spreadsheet
We can use the spreadsheet for the calculation. The calculation of a cell needs next four (4) cells, which are top, bottom, right, and left. The number of repeat is 1000 for the case. If we need the intermediate ones, it is necessary to use the number.
(3) Initial Conditions
It is assumed the middle of the long round bar, which represents the whole area, because the heating furnace is good in the temperature distribution in the longitudinal direction.
Time Difference: 0.001 second
Radius: 85 mm, Number of difference=20
Angle: Whole cirlce in radian. Numbner of differnence=21
Initial temperature of the rould billet= 300 degrees K.
Outside surface temperature of the billet=1000 degrees K.
Temperature of the furnace floor: 800 dengrees K.
(4) Temperature Simulation
Therre are two (2) ways. One is to program the difference equations and the initial conditions. Another is to use the functions of the spreadsheet. And then, repeat the necessary times of the calculation. It is necessary to repeat ten thousand (10 000) times for the case.
If we calculate the intermediate values as well, for example, we can obtain the temperature rising curve of the center of the billet.
It ended almost instantly for the 10 000 times of repetitive calculation. The specification of the lap to is corei5 4 cores, RAM 16GB.
(5) Outcome
(5)-1 Spreadsheet, Excel
The following table shows the spreadsheet of the t=10 seconds (10 000 times repetition)
(5)-2 Add-in 3D graph, Excel
The following graph is the add-in 3D graph. The original shape is round but the add-in is for the rectangular coordinate system.
The middle of the right end (r=85mm) shows the drop of temperature. It is the area, where the billet touches the furnace floor.
(5)-3 Rotation Matrix, 3D Graph
The following graph show the same oout come in the is shown in the scatter plot after conversion by the rotatin matrix. Please see the "3D Rotation" for detail.
Rotation condition is; sixty four (64) degrees in R(x) axis, minus 43 (-43) degrees in R(z) axis.
The axis of the scatter plot is hidden, because the data are converted by the rotation matrix. The additional data for the rotated axis are necessary if we draw the rotated axis. The vertical axis is tilted, and therefore, the values on the axis are wrong. The converted one is added.
The R(z) axis also tilts toward forward, therefore, the values in the vertical axis is incorrect. The values should be converted due to the tilt. The typed 1100 is the calculated one for reference.
The area where the round billet touches the floor is shown on the left side.
Author: T. Oda
The page was prepared in Excel, and automatic html and css generation by the "excel2web".