| |
 |
| |
 |
| ● アレクサンダー・ゲレジの本 訳 五弓勇雄先生 |
| ● マンネスマン穿孔 |
| 〇 材料の流れ |
| 〇 マンネスマン穿孔法 概要 |
| (1) ロールとのみ接触するゾーン |
| (2) ロールとプラグに接触するゾーン |
| (3) ロールとのみ接触するゾーン |
| 〇 ロール反力と動力の計算 |
| 〇 計算条件 |
| (1) 模式図 |
| (2) ロール、プラグ形状、セットアップ |
| 〇 計算結果 |
| 〇 熱間変形抵抗と摩擦係数の式 |
| |
 |
| ● アレクサンダー・ゲレジの本 訳 五弓勇雄先生 |
| |
| ゲレジは、マンネスマン穿孔法のロールの圧延反力と動力の計算をされているので、紹介します。 |
| |
| 計算式以外の部分、マンネスマン穿孔法の説明部分は小職の解釈なので、間違っているかもしれません。現役時代はこの考え方で大きな問題はなかったので、大きく外れている可能性は小さいと思います。 |
| |
 |
| ● マンネスマン穿孔 |
| |
| 「技術の話」「穿孔」で詳しく紹介していますが、19世紀の終わりに、磨き棒鋼の仕事をしていたドイツのマンネスマン兄弟は、設定を間違えると棒鋼の中心部が割れるトラブルに見舞われましたが、この現象をブラッシュアップして、高能率に穴をあける方法を見出したそうです。この方法がマンネスマン穿孔法と呼ばれる方法です。 |
| |
| 下の絵は、マンネスマン穿孔の模式図です。 |
| |
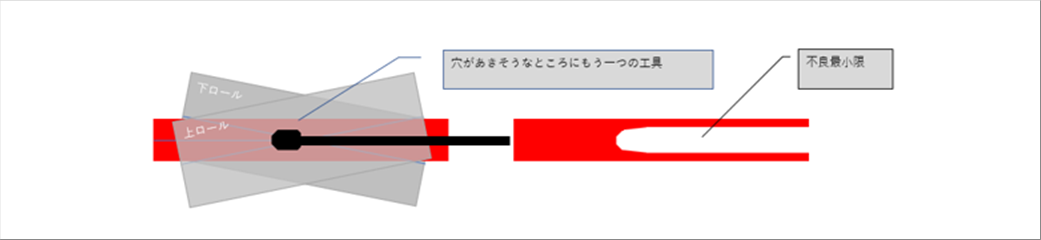 |
| |
| マンネスマン穿孔機は、1対の「樽型ロール」と、その中央に「プラグ」と呼ばれる工具、そのプラグを支える「バー」、絵にはありませんが、材料の位置をホールドするための1対の「シュー」で構成されています。 |
| |
| 横から見た実際の形状は、次のようになっています。 |
| |
| |
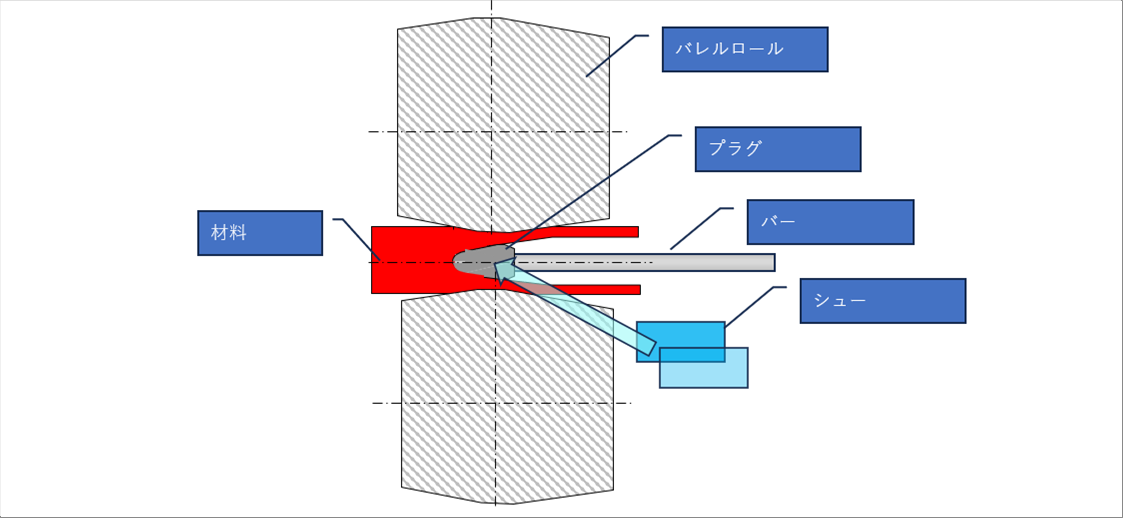 |
| |
| シューは、2個一組で、紙面に垂直な位置にあります。上の絵では、重ねると見にくいので、プラグの右下に描いてあります。 |
| |
 |
| 〇 材料の流れ |
| |
| マンネスマン穿孔は、材料は回転しています。上のロールとプラグで圧延された材料は、半回転して下ロールとプラグで圧延されます。半回転中は加工されないので、流れを定義するのは大変です。 |
| |
| 次の計算条件で、バレルロール、プラグ、材料肉厚を幾何学的に計算したものが次の絵です。 |
| |
| 計算条件:ロール胴径:1000mm、バレル角度:2deg、バレル中央並行部:60mm、プラグ径:142mm、プラグ先端位置:ロールセンターより170mm、ロール傾斜角度:10deg、材料外径:210mm、プラグ終端肉厚:25mm |
| |
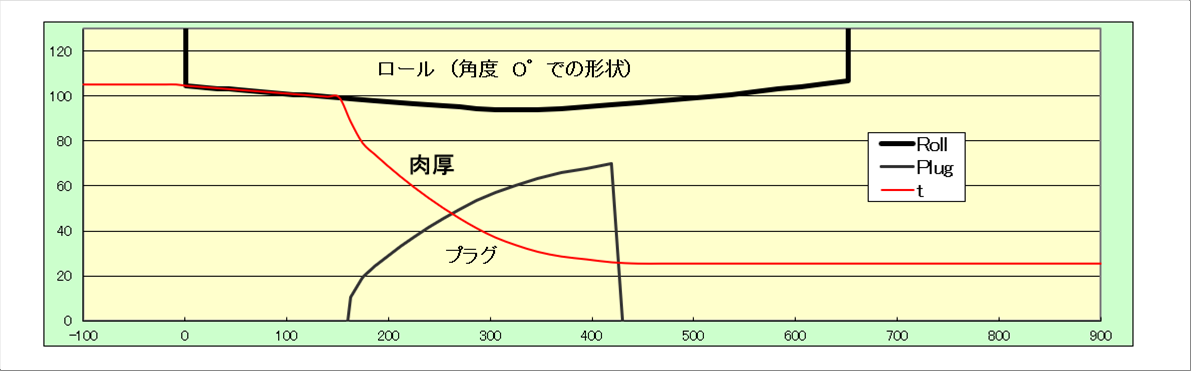 |
| |
| 注意: ロールは、傾斜角度0度で表示しました。 |
| |
 |
| 〇 マンネスマン穿孔法 概要 |
| |
| 上の絵の左側から材料が入ります。圧延の状態がいくつかに分かれるので、以下に説明します。 |
| |
| 下の絵は、それぞれの位置での材料の断面を示しています。 |
| |
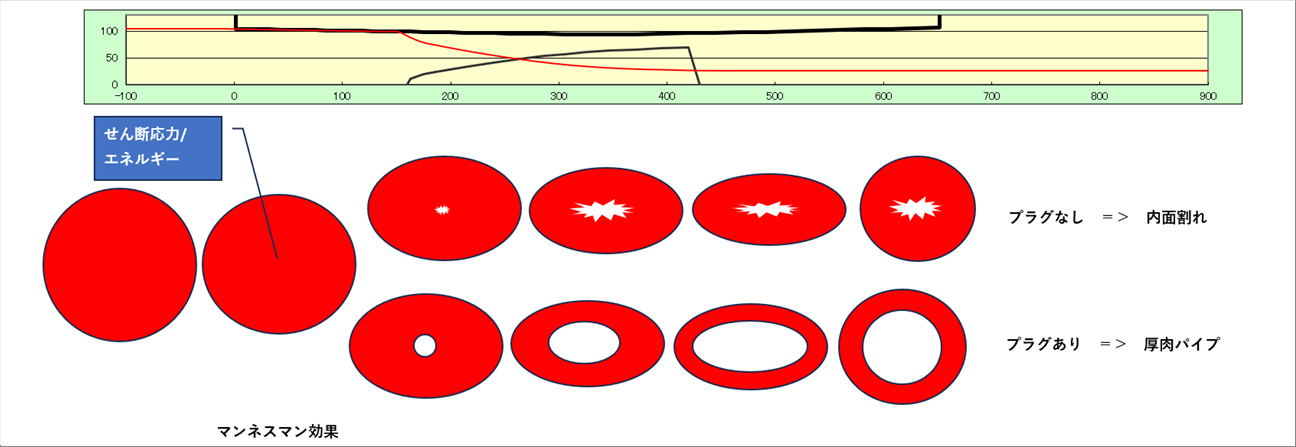 |
| |
| |
| (1) ロールとのみ接触するゾーン |
| |
| まず、材料とロールだけが接触する部分があります。材料は、ロールと接触すると、ロールの入側角度で若干小さくなります。この区間では、マンネスマン効果と呼ばれる、肉厚内部(絵では横軸上)に大きなせん断力とせん断歪がかかります。このせん断歪によって、せん断エネルギーが発生しています。 |
| |
| (2) ロールとプラグに接触するゾーン |
| |
| 3個目からは、上下に分かれていますが、上がプラグがない場合、下がプラグがある場合の模式図です。 |
| |
| 上が、プラグがない場合です。この場合は、中央部のせん断エネルギーが一定値になるか(ミーゼスの降伏条件)、せん断力が一定値になる(トレスカの降伏条件)と材料は降伏して、内部割れが発生します。(詳細は、塑性力学の基礎を参照ください。) |
| |
| 下がプラグがある場合で、マンネスマン穿孔法です。マンネスマン穿孔法では、割れが発生する直前にプラグがあるようにします。こうすることで、マンネスマン効果が利用でき、かつ、割れが発生する直前にプラグで圧延ができるので、内部割れを防止して、かつ、小さな力で圧延ができます。 |
| |
| プラグと接触してからは、大半径のロールと、小半径のプラグの異径ロール圧延が材料半回転ごとに行われます。圧延は、紙面に垂直な方向ですが、ロールの傾斜角分の斜め方向成分があります。 |
| |
| (3) ロールとのみ接触するゾーン |
| |
| プラグが終わると、材料はパイプになっていて、以降肉厚は変化しません。 |
| |
| プラグが終わっても、パイプはロールとしばらく接触しています。プラグとの最終圧延時点での外周長が、ロールと接触している区間で、徐々に丸くなるようにします。 |
| |
 |
| 〇 ロール反力と動力の計算 |
| |
 |
| 〇 計算条件 |
| |
| ゲレジの式は、幾何学的な形状、位置関係、材料寸法、パイプ寸法、材料温度だけで圧延反力と動力が計算できる。 |
| |
| (1) 模式図 |
| |
| 下図は、計算で使用する模式図で、プラグは円錐形となっている。 |
| |
 |
| |
| (2) ロール、プラグ形状、セットアップ |
| |
| 下の表で、ロール最大同径はロール中央部、最小同径は両端の数値。2段目の白抜き2か所、ロール平均径と圧延出側肉厚は計算値。 |
| |
 |
| |
| |
 |
| 〇 計算結果 |
| |
| 下の表が計算結果です。(計算が間違っていたら小職の責任です。) |
| |
 |
| |
| 〇 熱間変形抵抗と摩擦係数の式 |
| |
| なお、計算でネックになる変形抵抗と摩擦係数は、ゲレジの本では温度による式が書かれていたので、この計算以外でも使える可能性があるので式を転機しておきます。 |
| |
| 熱間変形抵抗 = 0.015 * (1400 - 穿孔温度) |
| |
| 摩擦係数 = 1.05 - 0.0005 * 穿孔温度 |
| |
| |
| Author : T. Oda |
| このページは、excel2webで自動作成しました。 |































