|
|
|
|
| ● 代表的な梁の反力、モーメント、たわみの公式 |
|
|
|
| ● 断面二次モーメント、断面係数の公式 |
|
|
|
| (1)矩形断面 |
|
|
|
| (2)円形断面 |
|
|
|
| (3)I型、C型、H型、U型断面 |
|
|
|
| ● 軸力、せん断力、曲げモーメントの符号 |
|
|
|
| ● 軸応力、せん断応力、曲げ応力 |
|
|
|
| ● 断面二次モーメントの定義と展開 |
|
|
|
| (1) 長方形断面の断面二次モーメントの計算 |
|
|
|
| (2) 円形断面の断面二次モーメントの計算 |
|
|
|
| ● 備考 梁の反力、モーメント、たわみ |
|
|
|
| (1) 荷重、反力、せん断力 |
|
|
|
| (2) モーメントM |
|
|
|
| (3) たわみ角y’、たわみy |
|
|
|
| (4) 公式の導出 |
|
|
|
| |
|
|
|
 |
|
|
|
| ● 代表的な梁の反力、モーメント、たわみの公式 |
|
|
|
| |
|
|
|
| 梁の固定方法と荷重方法の違いによって公式は変わるが、代表的な4種類をまとめると下のようになる。 |
|
|
|
| |
|
|
|
 |
|
|
|
| |
|
|
|
| この公式は、断面形状が四角形の場合だが、円形(棒状)、パイプ、四角パイプでは公式が異なる。各種断面の断面二次モーメントがわかればすぐ計算できるので、下に計算方法をまとめる。 |
|
|
|
| |
|
|
|
 |
|
|
|
| ● 断面二次モーメント、断面係数の公式 |
|
|
|
| |
|
|
|
| 断面二次モーメントは、その部材をどこで使うかによって変わりますが、ここでは図芯が断面内にある場合を示します。オフセットして使われる場合は、オフセットky堀の2乗に断面積をかけた分だけ大きくなります。(曲がりにくくなる。) |
|
|
|
| |
|
|
|
| 導出方法は下に書いておきますが、詳細は材料力学の基礎を参照してください。 |
|
|
|
| Ixオフセット = yo^2 A + Ix図芯 |
|
|
|
| |
|
|
|
| なお、断面二次モーメント Ix は、曲げモーメントがかかっていない方向(x方向)に部材がオフセットしても断面二次モーメントの係数は変わりません。したがって、部材の合計寸法が同じであれば、Ix は変わりません。 |
|
|
|
| |
|
|
|
 |
|
|
|
| ● 矩形断面 |
|
|
|
 |
|
|
|
| |
|
|
|
| パイプは、コーナーは直角ではなくカーブしているが、計算式では無視した。 |
|
|
|
| |
|
|
|
| パイプは、板厚が同じ場合が多いので、内寸法の代わりに、肉厚tを計測して内側寸法を計算するのが実用的だと思います。 |
|
|
|
| |
|
|
|
| a1 = a - 2t, b1 = b - 2t, h1 = h - 2t |
|
|
|
| |
|
|
|
 |
|
|
|
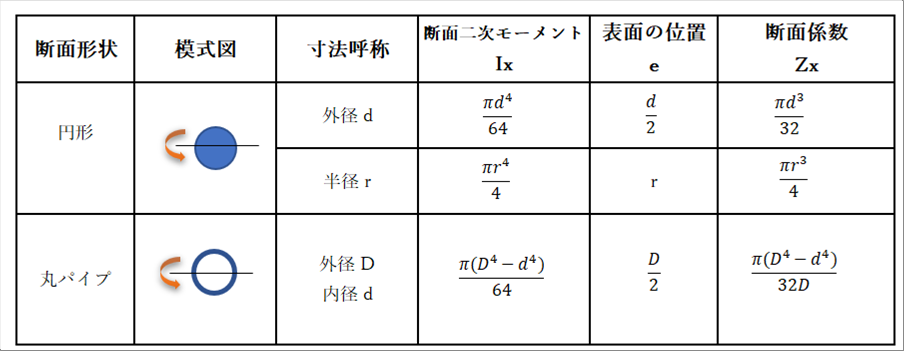
| ● 円形断面 |
|
|
|
 |
|
|
|
| |
|
|
|
 |
|
|
|
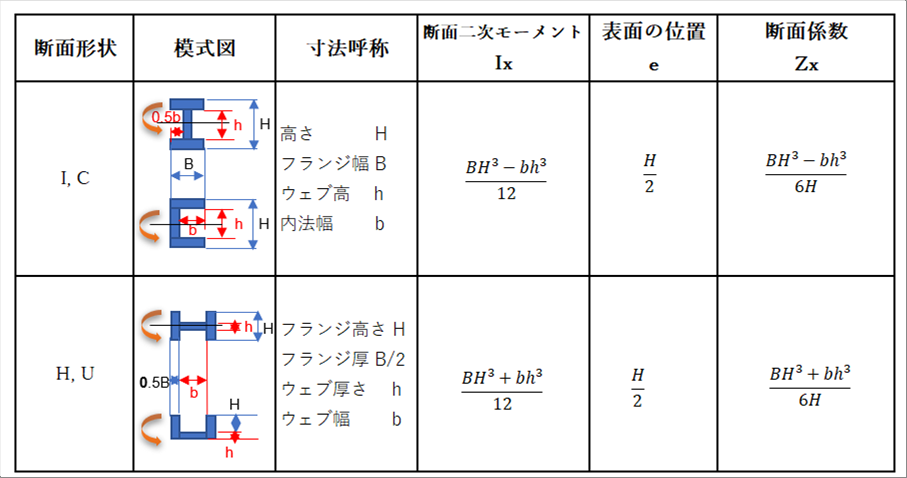
| ● I型、C型、H型、U型断面 |
|
|
|
 |
|
|
|
| |
|
|
|
| 例えばI型鋼では、フランジ内側はテーパー状だが、無視した。 |
|
|
|
| |
|
|
|
| I型とC型は、同じ式で表される。H型とU型も同じ式で表される。理由は、下の断面二次モーメントの定義と展開を参照方願います。 |
|
|
|
| |
|
|
|
 |
|
|
|
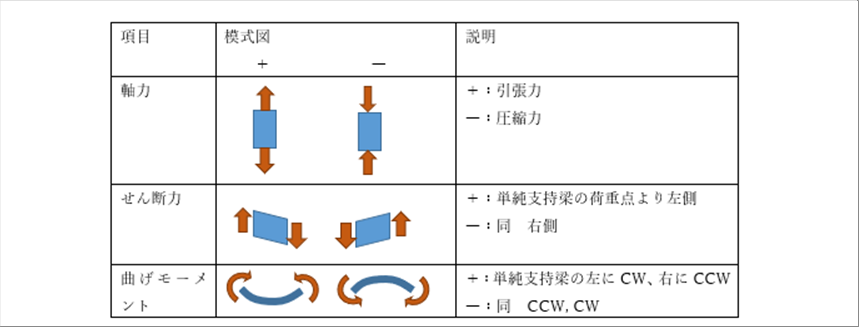
| ● 軸力、せん断力、曲げモーメントの符号 |
|
|
|
| 自分の中で決めても構わないと思いますが、一般的な符号は次の通りです。 |
|
|
|
| |
|
|
|
 |
|
|
|
| |
|
|
|
| 軸力と曲げモーメントの符号はそういうものだと、なんとなく納得がいきますが、せん断力は、位置が変わると符号が変わるので、せん断力の符号はわかりにくいと思います。せん断を知りたい位置で、プラスかマイナスかはを考えるときは、その場所で仮想的に切ってみます。 |
|
|
|
| |
|
|
|
 |
|
|
|
| |
|
|
|
 |
|
|
|
| ● 軸応力、せん断応力、曲げ応力 |
|
|
|
| |
|
|
|
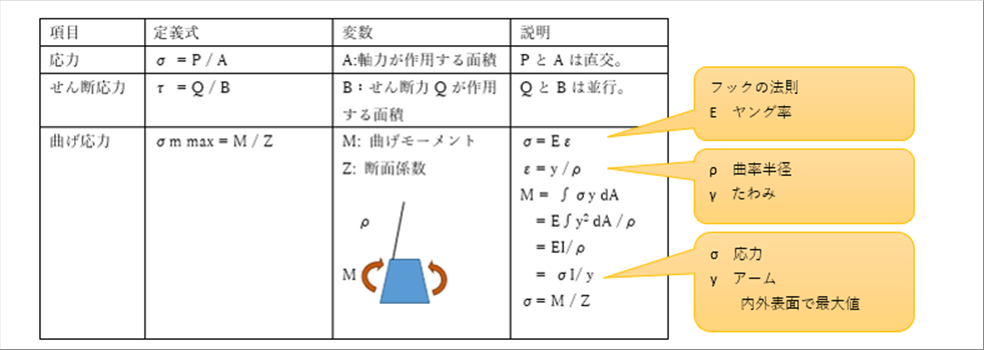
| 応力集中を考慮しない場合、応力、せん断応力は断面積内で一定なので、力を面積で割るだけです。 |
|
|
|
| 曲げ応力は、断面内で均一ではなく、プラスからマイナスまで場所によって変わります。これは、モーメントを割っている断面係数が、断面の形状と断面内の位置によって決まっているからです。詳細は材料力学の基礎を参照ください。 |
|
|
|
| |
|
|
|
 |
|
|
|
| 曲げモーメントによる応力は、内外表面で最大値になり、符号が逆になります。 |
|
|
|
| |
|
|
|
 |
|
|
|
| ● 断面二次モーメントの定義と展開 |
|
|
|
| |
|
|
|
| 梁の断面形状 |
|
|
|
| 正方形、長方形、長方形回転、円形、角パイプ、丸パイプ、まれに??、その他
H鋼、Iビーム |
|
|
|
| |
|
|
|
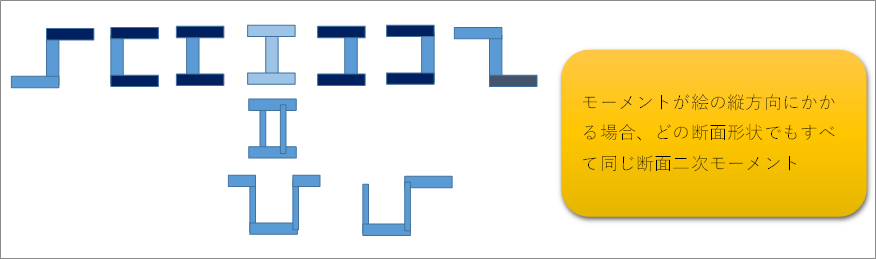
| X軸周りの断面二次モーメント |
|
|
|
| Ix=∫ y^2 dA
断面形状によって関数y(x)の式が変わる。 |
|
|
|
| |
|
|
|
 |
|
|
|
| |
|
|
|
| 形状y(x)の梁を、(x0, y0)オフセットして使う場合
Y=y+y0, X=x+x0を代入して、∫y dA=0, ∫x dA=0なので、
IX=∫Y2 dA = ∫(y+y0)2 dA = y02A+Ix |
|
|
|
| |
|
|
|
 |
|
|
|
| (1) 長方形断面の断面二次モーメントの計算 |
|
|
|
| |
|
|
|
 |
|
|
|
| |
|
|
|
 |
|
|
|
| (2) 円形断面の断面二次モーメントの計算 |
|
|
|
| |
|
|
|
 |
|
|
|
| |
|
|
|
 |
|
|
|
| ● 備考 梁の反力、モーメント、たわみ |
|
|
|
| |
|
|
|
 |
|
|
|
| (1) 荷重、反力、せん断力 |
|
|
|
| |
|
|
|
| 荷重には集中荷重Pと分布荷重wがある。これと釣り合うべく、梁の支点で反力Rとせん断力Q が発生する。 |
|
|
|
| |
|
|
|
 |
|
|
|
| (2) モーメントM |
|
|
|
| |
|
|
|
| 梁のどちらか一方の端部Aを決めて、そこからの距離xでモーメントM(x)が発生する |
|
|
|
| |
|
|
|
 |
|
|
|
| (3) たわみ角y’、たわみy |
|
|
|
| |
|
|
|
| モーメントM(x)に応じてたわみ角y(x)’が発生し、たわみ角y(x)’が連続的につながって各部分のたわみy(x)となる。たわみとモーメントの関係式は下記。 |
|
|
|
| y(x)’’= - M(x)/EI |
|
|
|
| |
|
|
|
 |
|
|
|
| (4) 公式の導出 |
|
|
|
| |
|
|
|
| 変数が複数個ある連立方程式になるが、梁の両端部の固定方法と、荷重点での角度y’とたわみ量yの境界条件も同数あるので、連立方程式を解くことができる。 |
|
|
|
| |
|
|
|
| モーメントM(x)はxの3乗程度の関数なので、微分方程式は容易に積分できる。境界条件をあてはめて、公式が導出できる。 |
|
|
|
| |
|
|
|
| |
|
|
|
| Author: T. Oda |
|
|
|
| このページは、excel2webで自動作成しました。 |
|
|
|