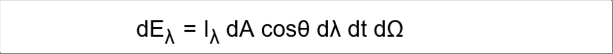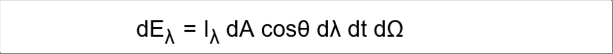熱輻射　Heat Radiation
●　真空中でも熱は伝わるのか
●　熱伝導、熱伝達のおさらいと熱伝導と電磁気学との接点
どういう物体が電磁波を放出しているのか
電磁波はどこに向かうのか
●　放射フラックスと形態係数
●　放射エネルギーの計算方法
●　黒体のエネルギー放射の式
放射束密度（放射フラックス）
レーリーとジーンズの公式とウィーンの公式
プランクの法則
ステファン・ボルツマンの法則
●　輻射熱の計算
シミュレーションでの注意
各種材料の温度、表面性状による輻射率
●　真空中でも熱は伝わるのか
「真空断熱技術」を利用したタンブラー、カップ、水筒などが市販されているが、TIGERさんのホームページの説明を読むと、「真空断熱技術」ではなく「真空・断熱技術」と書いてあり、真空にして断熱できるのは熱伝導と熱伝達で、熱輻射は真空でも防げないので、輻射熱を反射する鏡を使っていますと書いてある。伝熱の仕組みを端的に書いてあるので一読がおすすめです。https://www.tiger.jp/b2b/about_dannetsu.html
熱は、粒子の振動運動エネルギーと、電磁波の波長に応じたエネルギーで成り立っていますので、エネルギーのひとつの形態です。
真空には粒子が存在しないので、振動エネルギーは伝わりませんが、電磁波は伝わります。この、電磁波による伝熱を熱輻射といいます。
●　熱伝導、熱伝達のおさらいと熱伝導と電磁気学との接点
ー　物体がほかの物体に接していると、熱輻射に加えて分子（原子）の振動が直接伝わります。物体に温度分布がある場合は、その物体内で振動が伝わります。前者を熱伝達、後者が熱伝導です。
ー　金属は陽子と同数の電子をもち、電子は気体のように金属内で自由に動きます。この動きにより、気体の熱伝達のように金属内で熱を伝えます。このため、電気伝導率が高い金属は熱伝導率も高いです。
●　どういう物体が電磁波を放出しているのか
日常生活では、電磁波を出しているのは携帯電話、テレビ局などで、カレーやラーメン、眼鏡などは、電磁波を出していないと思われがちですが、あらゆる物体は電磁波を放出しています。
テレビ塔、スマホが電磁波を出しているのはいいとして、カレー、ラーメン、眼鏡も電磁波を出しています。
にわかには信じがたいですが、物体を作っている最小単位を見ていくと納得がいきます。カレーライスはルー、野菜、肉、ライスなど構成物質が多いですが、（たぶん）カレーライスの主成分である水を考えます。水以外のほかの具材が電磁波を出しているかどうかも、同様に考えられます。
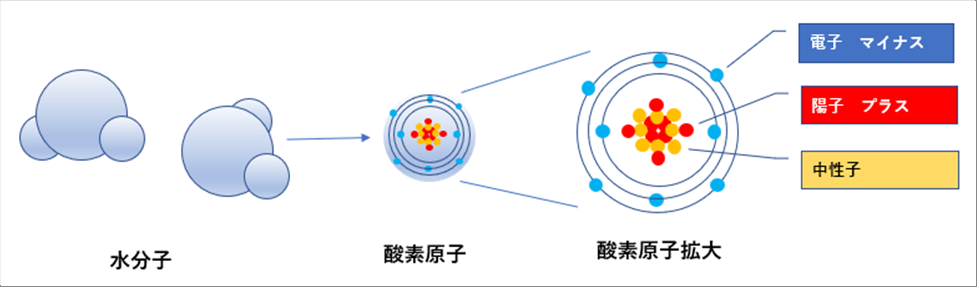
水がある温度になっているとします。これを分子、原子で考えてみます。水は、水分子の集まりです。水分子は水素原子と酸素原子で構成され、それらの原子は、陽子、電子、中性子でできています。
分子の振動が熱（エネルギー）で、熱の程度が温度です。したがって、水がある温度です時は、水分子がその温度に応じて振動していることになります。水分子が振動しているということは、酸素と水素の原子も振動していることになります。
原子は、陽子、電子、中性子でできています。陽子はプラス、電子はマイナスの電荷をもつので、原子が振動しているとは、プラスとマイナスが近くで振動していることになります。
プラスとマイナスが近くで振動していると、電磁波を放出します。したがって、温度がある物体はすべて電磁波を放出しています。温度が高いほど分子（原子）振動が激しいので、熱輻射の放出エネルギーもおおきくなります。
なお、プラスとマイナスが近くで振動していると電磁波を放出するのは、電磁気学の範疇なので割愛します。興味がある方は、「近接場理論」などで検索するとわかると思います。
したがって、すべての物質は電磁波を放出していますので、カレー、ラーメン、眼鏡も電磁波を放出しています。
●　電磁波はどこに向かうのか
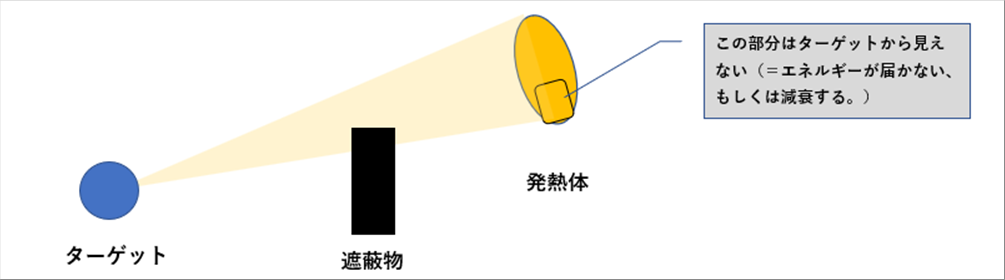
スマホ、テレビ電波塔と同じく、あらゆる物体から出た電磁波は、あらゆる方向に向かっています。
途中に遮蔽物があると、さえぎられたり、減衰したりします。
●　放射フラックスと形態係数
熱力学的に考えると、ある場所にあるターゲットから見たら、放射エネルギーのうち、どれだけが受信できるかが重要です。これを放射束密度（放射フラックス）といいます。
さらに、電磁波はなにかに反射してターゲットに届く場合もあれば、何かで遮られてターゲットに届かない場合もあります。これを表現するものを形態係数といいます。（詳細は形態係数を参照してください。）
●　放射エネルギーの計算方法
熱力学なのに電磁波が出てくる理由がわかったところで、電磁波の基本式を考えます。輻射を考えるときにこれらの知識は重要なので、書いておきます。
有名なところでは、波長λ、振動数ν、光速度ｃの関係ですが、下式で与えられます。真空中ではｃは一定値なので、波長と振動数のどちらかがわかればよいので、未知数が一つ減ります。また、この式で、積分範囲を周波数と振動数とで変換することも可能です。計算結果やグラフは、見やすいほうを選択すればいいです。（　ｃ＝νλ　）
放射エネルギーを全波長領域、全方位で積分して黒体の放射エネルギーが求められます。有名なステファン・ボルツマンの法則で、「放射エネルギーは絶対温度の4乗に比例する。」という極めて覚えやすい式です。この比例定数がステファン・ボルツマン係数です。
黒体輻射エネルギ＝σT^4
σ：ステファンボルツマン係数
この式は、入った電磁波をすべて吸収する黒体（詳細は熱力学基礎参照）や、無限平板などで理想的な状態で適用できます。
加熱炉、熱処理炉はど実在の物体は、入射エネルギーの一部を反射し、設計寸法があり、壁面が傾斜している場合もあります。実際に使うためには、黒体の放射強度（＝最大値）に輻射率（＝吸収率）と、物体の形状・位置に応じた係数と表面積を乗算して求められます。
輻射熱（吸収熱）＝形態係数ｘ輻射率ｘ面積ｘσT^4
●　黒体のエネルギー放射の式
黒体のエネルギー放射が最大値なので、理解しておくためにまとめました。
黒体とは
すべての波長の電磁波を完全に吸収する理想物体を黒体といい、黒体は同じ温度ではほかのどの物体よりも大きな放射を出すことができる。黒体の放射は絶対温度のみに依存する。
ー　真空中の電磁場
真空中の電磁場は、マクスウェルの方程式を使うと計算でき、単位体積当たりの微小振動数中の、固有振動数の量の微分方程式が得られます。
ー　スペクトル
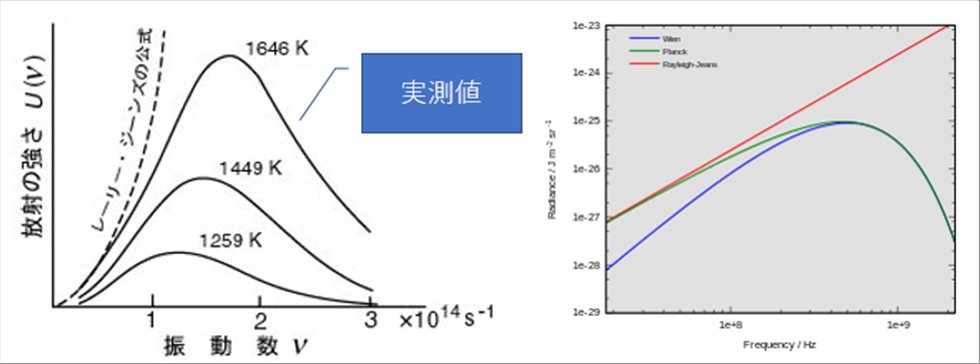
電磁波（可視光も電磁波）の振動数ごとの強度分布をスペクトルいいます。同じ物質のスペクトルは、物質の温度が変わると変化します。スペクトルを数式で表現する方法が数のようにいくつか提案され、いくつかの法則を統合した形のプランクの法則が有名です。
ー　放射強度の定義式
いくつかの式が提案され、低い振動数でよくあうレーリーとジーンズの法則と、高い振動数の領域でよくあうウィーンの公式の両方を満たす、プランクの法則が広い振動数の領域でよくあうと言われています。
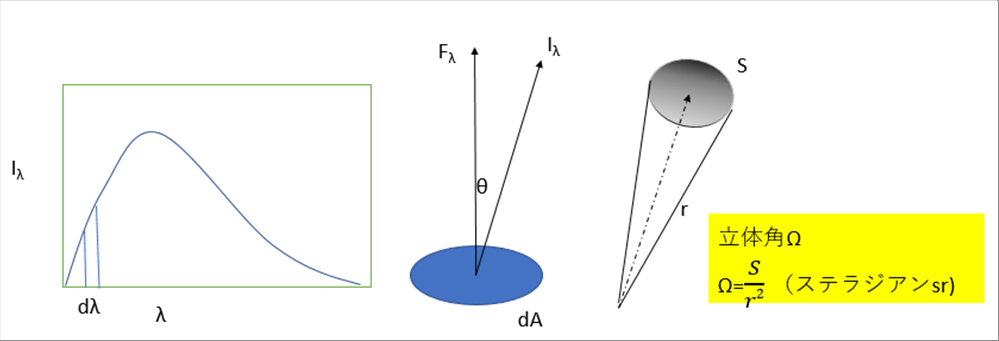
物体の表面dAから、θの方向の立体角dΩに進む放射に、波長λからλ+dλの範囲で時間dtあたりの放射エネルギーdEλは、
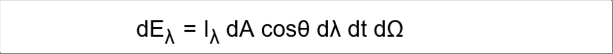dEλ=IλdAcosθdλdtdΩ
放射強度は、
Iλ = dEλ / dAcosΘdλdt dΩ W/m2srμm
●　放射束密度（放射フラックス）
全放射強度は、全周波数で積分して求めます。
I = ∫ Iλ dλ
放射束密度強度（放射フラックス）は、放射強度法線方向（半径方向）への放射エネルギーなので、次式となります。
Fλ = π Iλ
放射面の放射強度が一定の場合、鉛直の位置が放射面全域から受ける放射はπ倍となります。（π倍するのはよく忘れますので、忘れないようにしましょう。個人的な失敗例より。。。）
●　レーリーとジーンズの公式とウィーンの公式
マクスウェルの電磁気学によれば、単位体積当たりの微小振動数中の、固有振動数の量の微分方程式が得られます。（電磁気学の話ではないので詳細は省略）これらの固有振動数に、一定量ずつのエネルギー（程度は温度で表記できる）が分配されていると仮定します。そうすると、ある温度の物体の電磁波（光）の振動数と強度がわかれば微分方程式が完成します。すなわち、物体のスペクトルを計測すれば微分方程式が完成します。
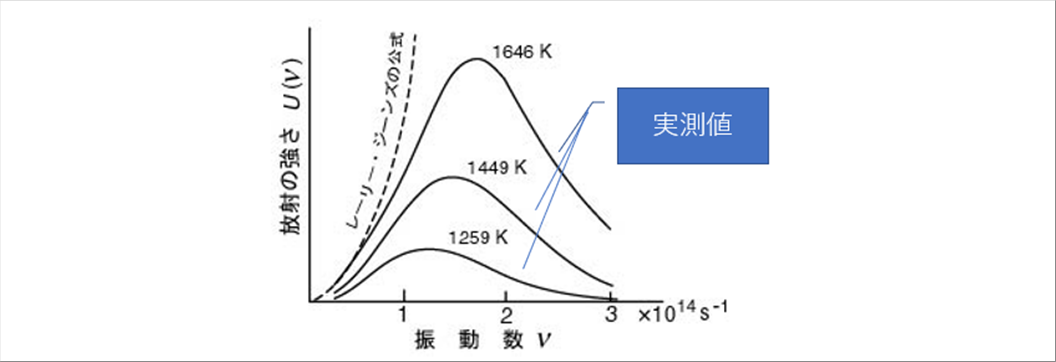
ー　レーリーとジーンズの公式
この公式は、振動数が小さいと成り立ちますが、振動数が大きくなると成り立たちません。
ー　ウィーンの公式
黒体からの放射エネルギーは、温度T、振動数νとある関数Fであらわされるとします。ウィーンの公式は、Fをある式にすると、低い振動数では成り立ちませんが、高い振動数の領域で成り立ちます。（＝実験値とよくあいます。）
●　プランクの法則
ウィーンの公式の関数Fを
F(x) = κβ / (exp(βx) - 1 )
と置いて、βを実測とよく合うように決めると、実測と低い振動数から高い振動数までよく合うことを見つけた。分子のkβ=hと書いて、hをプランク定数といいます。kはボルツマン定数。
h=6.62607 x 10^(-34) Js, k=1.38065 x 10^(-23) J/K
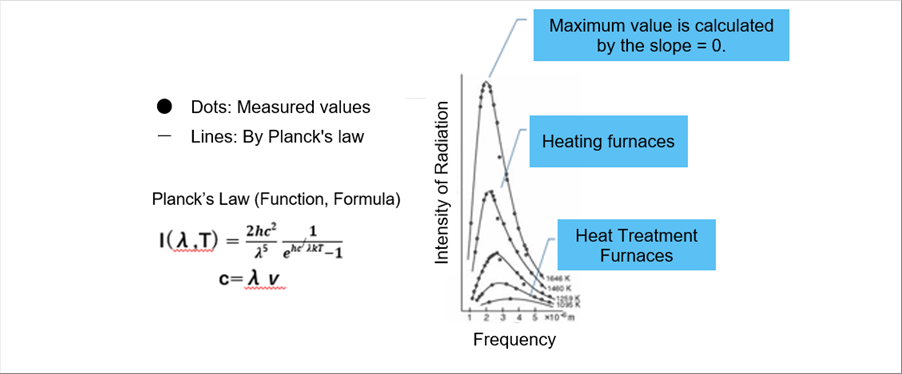I(λ,T) = 2hc^2/^5 . 1 / (exp(hc/λκT) - 1 )
プランクの法則で重要なことは、温度Tが決まると、波長λ（振動数ν）に対応する放射強度が決まるということです。温度シミュレーションに大変便利です。
●　ステファン・ボルツマンの法則
全放射量は、プランク関数を全波長で積分して求めます。
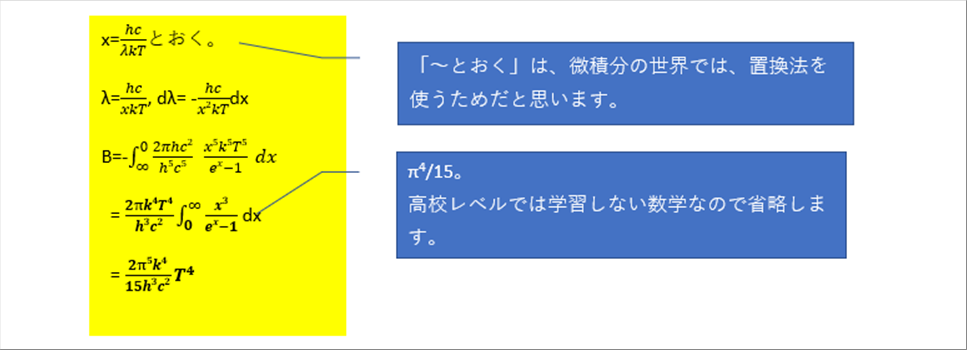
次式がステファン・ボルツマンの法則です。積分の概要をその下に記します。
結論は、全放射量は、絶対温度の4乗に比例するという有名な式になります。
放射フラックスは、次式で計算できます。Πの乗算を忘れないでください。
F(T) = πB(T)
なお、低温では赤外線、高温では紫外線がメインなど、温度によってスペクトルの分布パターンが違いますが、全波長で積分しているので、スペクトルの差によらず同じ式が適用できます。
●　輻射熱の計算
物体の輻射熱（放射能）は、全放射量に放射率をかけて求めます。
黒体の放射能　E(W/m2) =εσT^4
ε: 放射率（輻射率）
σ：ステファンボルツマン係数 5.67x10-8 W/m2K4
T: 物体表面温度 K 高温TU, 低温TLの場合は、 TU^ 4- TL^ 4
輻射熱量　Q(W)=EA
A:　表面積 m2
形態係数
シミュレーションでの注意
輻射熱量は、絶対温度の4乗に比例するので、面積が大きく、または、高温であればあるほど大きくなります。加熱炉、熱処理炉など、徐々に温度を上げていく場合は、高温ゾーンでは被加熱材への入熱のメインになると思われる。また、輻射率は、実際のの輻射率を使うことが重要となります。
●　各種材料の温度、表面性状による輻射率
輻射率は放射温度計の取扱説明書に書いてあるので、参考にするといいでしょう。
ただし、輻射率は、物体の材質、物体の温度と表面性状によって大きく違うので、取説の値を参考にしつつ、接触温度計との比較を行って決める必要があると思われる。
Author: T. Oda
このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。