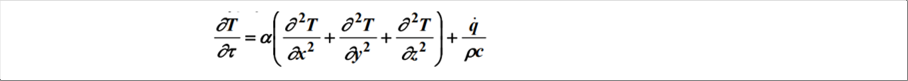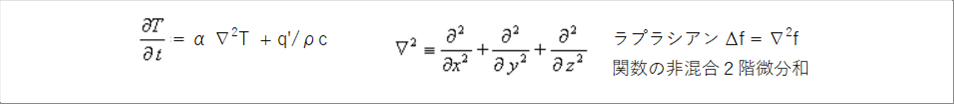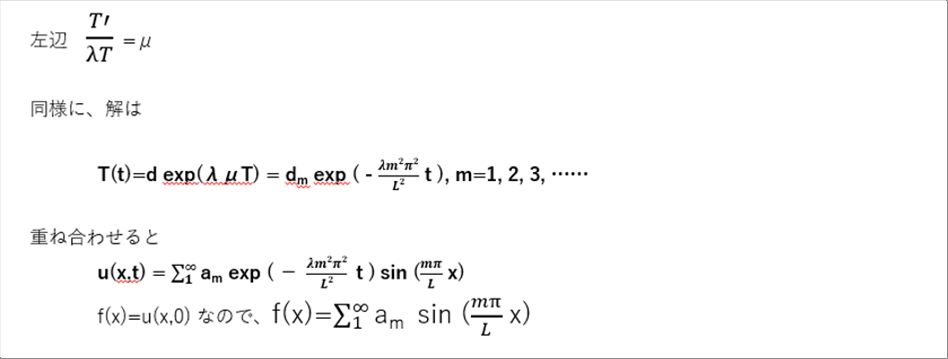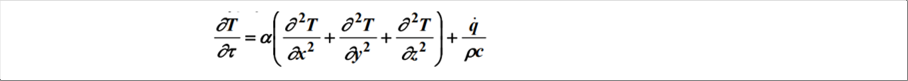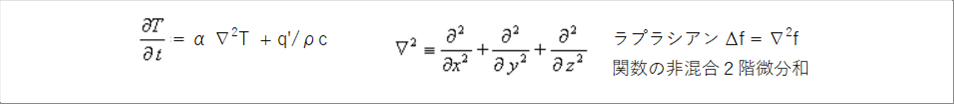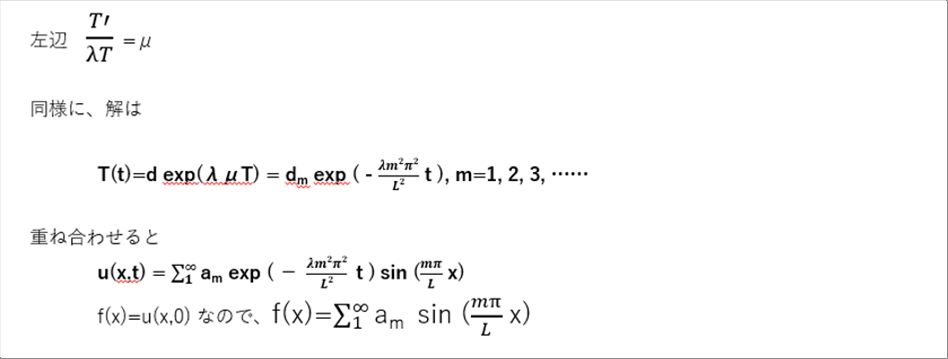|
 |
| ● 目的 |
| ● フーリエの法則 |
| ● 熱伝導方程式 |
| ● 熱伝導方程式の解 |
| 解析解の手順 |
| 解析解とグラフ |
| |
 |
| ● 目的 |
| |
| 熱伝導方程式、波動方程式は、例外的に特別な場合を除き解析的に解を得ることはできません。このため、実務では、差分法などの数値計算で逐次計算します。解析的な解が得られないので誤差が心配になりますが、誤差は差分の一次式になるので、差分を十分小さくとれば、誤差は十分小さくできることが証明されています。 |
| |
| 差分法詳細: 差分法参照 |
| |
| 熱伝導方程式が例外的に解けるのは、解u(x,t)が温度だけの式T(t)と位置のみの式X(x)の積で表現できる場合 u(x,t)=T(t)X(x) が有名です。この式で実際に制御している炉は皆無(だと思います)が、考え方の参考になるので紹介したいと思います。 |
| |
 |
| ● フーリエの法則 |
| |
| フーリエの法則は、フーリエの冷却則として、ストーリーの熱力学基礎でも紹介しましたが、シミュレーションで使えるように式で紹介したいと思います。ちなみに、式と解法は、19世紀に提案されました。 |
| |
| 物質内では、常時熱エネルギーが移動しています。移動方向は、温度の高いところから低いところです。熱の移動を法則化したものがフーリエの法則です。 |
| |
| フーリエの法則は、単位時間に、単位面積を通って流れる熱量qは、温度勾配に比例するというものです。「温度勾配」というととっつきにくい方もいると思いますが、「温度差」です。温度差が大きいほど流れる熱量は大きくなります。 |
| |
| アルミ製の箸を淹れたてのコーヒーにつけた場合と、淹れてから時間がたって室温と同じくらいに冷めてしまった場合で、10秒後の箸を持つ手の熱さを比較します。淹れたてのコーヒーにつけた場合のほうが熱いです。これは、淹れたてのコーヒーとの温度差が冷めたコーヒーより大きいからです。 |
| |
| アルミ製の箸を漆の箸にします。アルミ製の箸に比べて漆の箸のほうが、熱くありません。これは、アルミより漆のほうが熱を伝えにくいからです。 |
| |
| このように、温度差の大小で熱の伝わり方が違い、さらに、温度差が同じでも材料が変わると熱の伝わり方に差が出ます。この時の比例定数λを熱伝導率 heat conductivity といいます。 |
| |
| q = - λ ∂T/ ∂x |
 |
| |
| 符号がマイナスなのは、温度の高いところから低いところへ移動する方向を表しています。実際の生活では温度差が明確なので符号を気にしなくても熱の移動方向を間違えることはありませんが、温度シミュレーションをする際には、高温部がどこになるかは明確にわからない場合があるので、符号は重要になります。 |
| |
| 熱量の単位はJなので、qの単位はJ/(sec.m2) = W/m2になります。温度勾配∂T/∂xの単位はK/mなので、熱伝導率λの単位は W/m2 / (K/m) = W/(m.K)になります。 |
| |
 |
| ● 熱伝導方程式 |
| |
| 微小領域のエネルギーのつり合いから、熱伝導方程式を求めることができます。熱とエネルギーは同じものですが、言葉としてわかりやすいように熱は出たり入ったり発生したりして、エネルギーは内部にたまるものとして書くと次のようになります。 |
| |
| 入熱 + 発熱 = 内部エネルギーの増減 + 出ていく熱 |
| |
| (1) 微小領域は、dx、dy、dz |
| (2) x方向 入熱 = qx dy dz (q:熱、qx:位置xでの入熱) |
| (3) 出ていく熱は位置xがx+dxに代わります。= q x+dx dy dz。 |
| (4) 発熱は、q' dx dy dz (q': 微小体積内の熱量の変化速度) |
| 物体の運動方程式では、位置の時間微分が速度です。熱の場合も似ており、温度の時間微分が熱エネルギーなので、次式が得られます。 |
| (5) 内部エネルギーの増減 = ρc ∂T/∂t dx dy dz |
| |
 |
| |
| y方向、z方向も同様なので、x、y、z全体では次のようになります。 |
| |
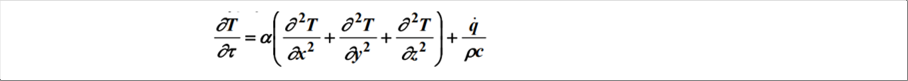 |
| |
| 微分方程式は長いので、ナブラ演算子を使うと下記のようになります。 |
| |
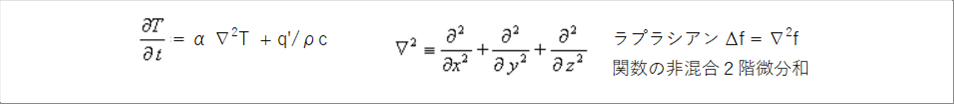 |
| |
 |
| ● 熱伝導方程式の解 |
| |
| 熱伝導方程式は、一般的には解けません。解く方法で有名なのが変数分離法と呼ばれるものです。 |
| |
| フーリエの法則を使って得られた熱伝導方程式の解析解を得るための手順は次の通りです。 |
| |
 |
| |
| (0)熱伝導方程式で、発熱q'=0、かつ、1次元とする。 |
| (1)解析解(元の式)uは、tだけの関数T(t)とxだけの関数X(x)の積と仮定する。 |
| (2)式を変形して、右辺がTの式、左辺がXの式になるようにする。 |
| (3)Tの式とXの式が等しいのは、それれが同じ定数の場合に限られる。 |
| (4)右辺と左辺を個別に解く。 |
| |
| q'=0の1次元の熱伝導方程式は、右辺が2階微分、左辺は1階微分となっています。微積分の基礎として、2回微分して元の式に戻るのは三角関数(sin、 cos)で、1回微分すると元の式にもどるのは、exp(x)なので、なんとなくどういう展開になりそうかわかりますよね。 |
| |
 |
| |
| 具体的には、次のようになります。 |
| |
| (0)から(3)まで |
| |
 |
| |
| (4)の右辺 |
| |
 |
| |
| (4)の左辺 |
| |
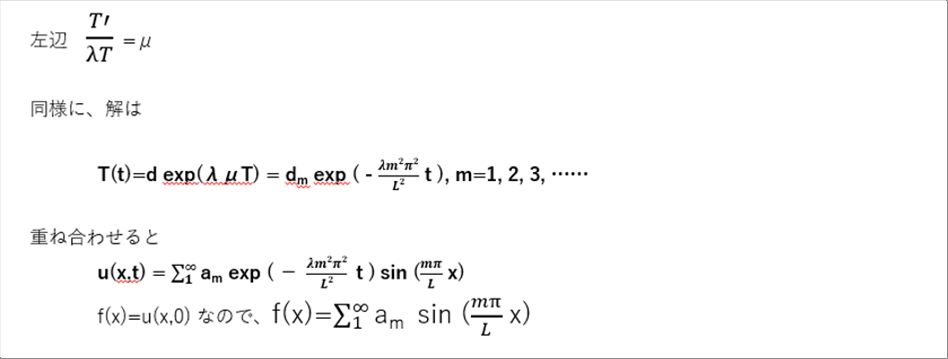 |
| |
| うえのsinだけの無限級数和は、いわゆるフーリエ正弦級数と呼ばれるもので、興味がある方は専門書、解説しているサイトなどを参照ください。 |
| |
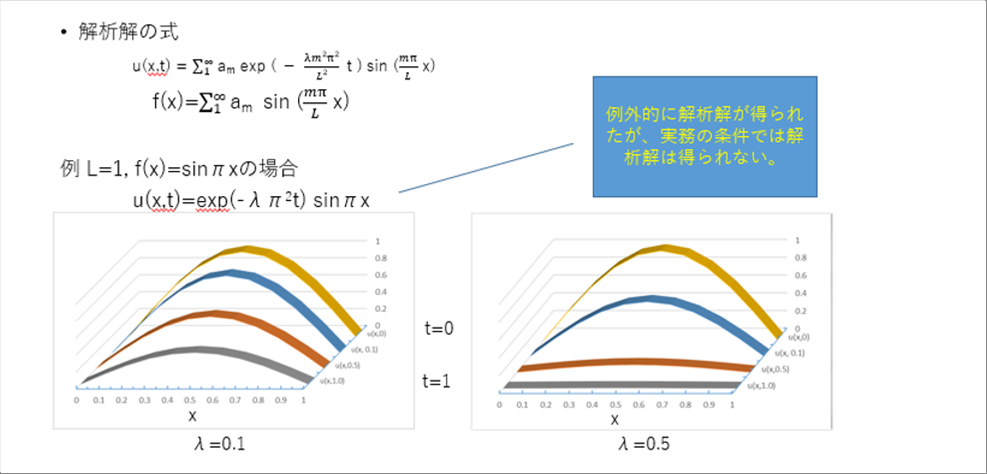 |
| |
| この解析結果を使って何かの温度計算をすることは、まずないと思いますが、我々の大先輩が19世紀に研究されたご苦労は偲べると思います。 |
| |
| 当時と違い、パソコンで、3次元、実際の使用環境に合わせたシミュレーションができるので、数値解析はシミュレーション SIM を参照ください。 |
| |
| Author: T. Oda |
| このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。 |