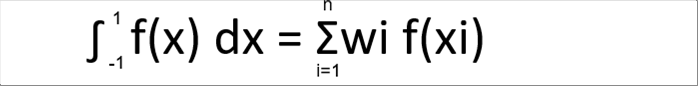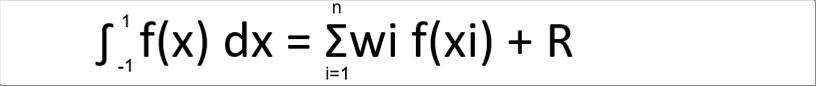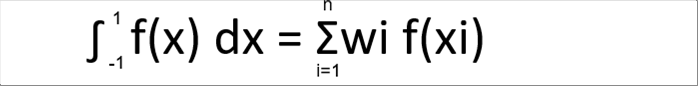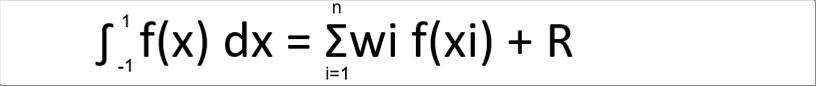| |
 |
| |
 |
| ● 数値積分 |
| ● ガウス・ルジャンドルの数値積分 |
| 代表位置と重み |
| 計算例 |
| 誤差 |
| ● 積分範囲の変更 |
 |
| ● 数値積分 |
| |
| 熱伝導方程式、流体の運動方程式などの微分方程式は、左辺が時間の1階微分、右辺が位置の2階微分などで、例外的に特殊な場合以外は、積分して解析的に解くことはできません。例外的に解ける場合は変数分離法が有名で、このホームページでも紹介していますが、実際の装置、設備には適用できません。このため、有限要素法、差分法などの近似解が開発されています。これらは近似解なので、誤差がありますが、誤差を十分小さくする方法も見出されています。現在では、十分実用に耐えるものとして広く認識されています。 |
| |
| 差分法は、微分方程式をテイラー展開して無限級数で直接近似するので、積分は必要ありません。有限要素法は、要素内に適用する関数を決めて、節点数分の他元連立方程式を解きます。解く際に、関数を積分する必要があります。 |
| |
| 数値積分の利点は、要素内の関数が積分できない場合に解が得られることと、積分できる場合でも同等の解が得られるので、同じプログラムが使える点です。数値積分は誤差が発生しますが、実用に差し支えないレベルまで小さくすることができます。 |
| |
| ここでは、ガウス・ルジャンドルの数値積分の紹介と、積分した場合との誤差を比較します。 |
| |
| |
 |
| 〇 ガウス・ルジャンドルの数値積分 |
| |
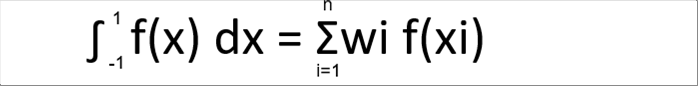 |
| |
| 上の式がガウス・ルジャンドルの数値積分の式です。導出方法は割愛させていただきます。f(x)が積分できなくても、f(xi)の値に係数をかけたものをいつくか合計するだけで積分値が得られます。 |
| |
| ここで、 |
| |
| f(x): 関数 (有限要素法なら、要素内に適用する関数) |
| |
| wi: 重み |
| |
| ∫ 積分範囲 ー1から+1まで |
| |
| Σ 合計範囲 i=1 から n まで |
| |
| |
 |
| 〇 代表位置と重み |
| |
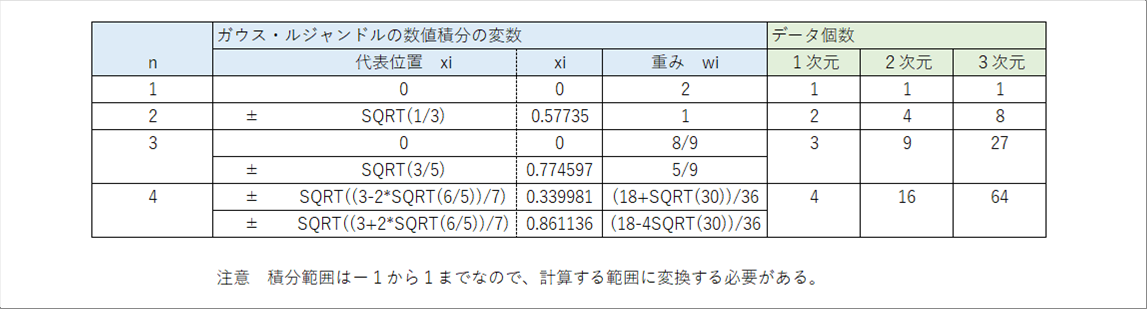
| n=4までの、代表位置 xi と、重み wi は、下の表で与えられます。 |
| |
 |
| |
| 2次元、3次元の場合は、それぞれの変数についてxiに相当する位置の数値を使うので、n=4の場合、2次元では16点、3次元では64点の合計値になりますが、プログラムを組む場合は、それぞれの変数でループすればいいと思います。 |
| |
 |
| 〇 計算例 |
| |
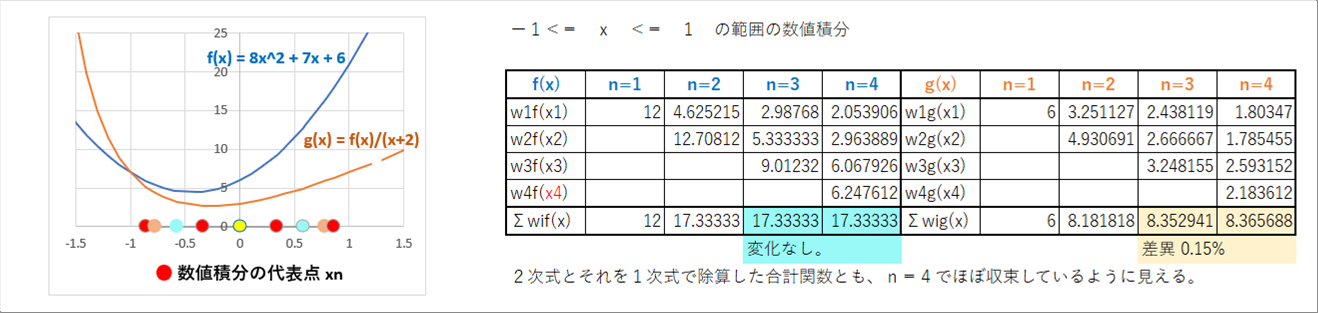
| 例として、単純な2次関数と、それを1次関数で除算した関数(特異点ができます。)の、n=4までを計算しました。グラフの下のサークルは代表点の位置を表しています。 |
| |
 |
| |
| グラフは、それぞれの関数と、数値積分の代表点を示しています。その横の表は、数値積分の計算結果を示します。例の2式は基本的な関数なので、式を積分して計算することは容易ですが、数値積分で計算することもできす。プログラム的には、どの式にも数値積分を使うほうが便利だと思います。(基本的な関数の微積分は、「技術の話」「微積分」参照ください。) |
| |
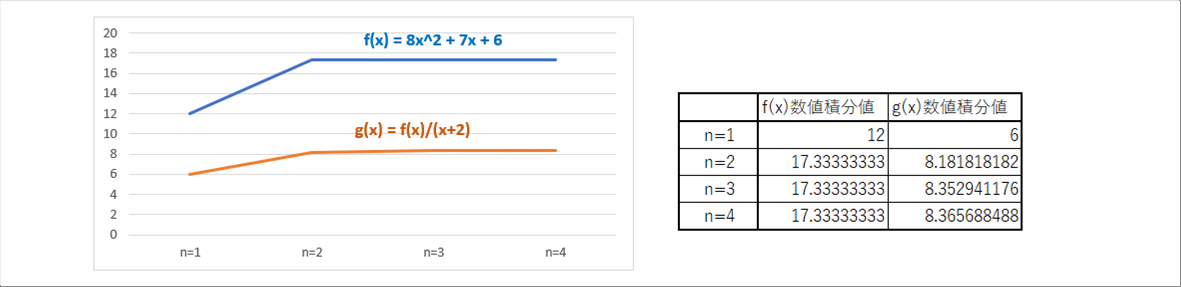
| 参考までにn=1からn=4までの数値積分値変化のグラフを示します。n=3以降では、ほとんど変化していないことがわかると思います。詳しくは、下の誤差を参照ください。 |
| |
 |
| |
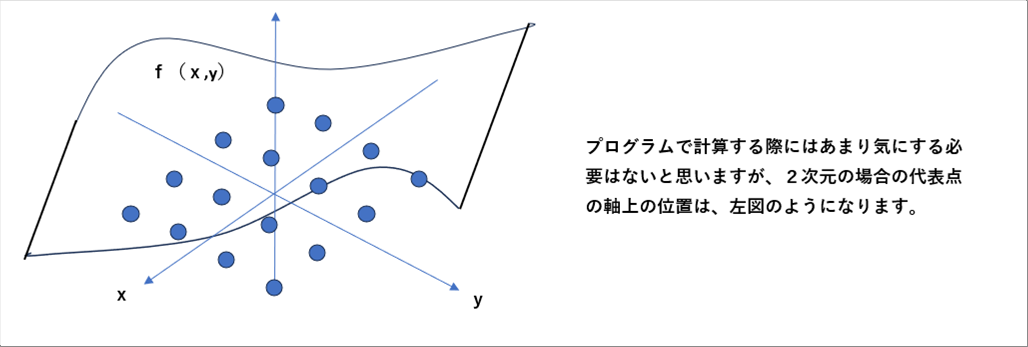
| 2次元でn=4の場合は、下の絵のように代表点の数は16点になります。 |
| |
 |
| |
| 3次元ではさらに増えて64か所になります。 |
| |
 |
| 〇 誤差 |
| |
| ガウス・ルジャンドルの数値積分の式の誤差を含むと次のような式になります。 |
| |
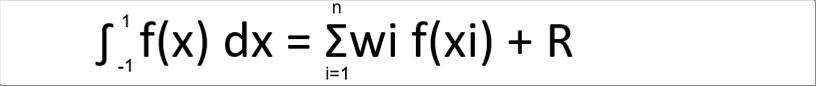 |
| |
| ここで、誤差 R は、 fの2n階微分に比例します。 |
| |
| (2n-1)次式は、2n階微分でゼロになるので、誤差もゼロになります。したがって、n = 4の場合は、7次式までの誤差はゼロになります。上の例のg(x)は、f(x)/(x+2)なので、n=4でも若干の誤差を含んでいます。 |
| |
| ガウス・ルジャンドル数値積分を使う場合は、n=3とn=4を計算して、同じ数値か、変化が小さいことを確認するのがお勧めです。 |
| |
| |
| 個人的な意見ですが、5次式までならn=3で誤差ゼロになるので、n=3でも実用上差し支えないレベルだと思います。 |
| |
 |
| 〇 積分範囲の変更 |
| |
| ガウス・ルジャンドルの数値積分の積分範囲はー1から1までですが、範囲を変更する場合は、置換積分をして式の変形をすれば、積分範囲の変更ができます。(置換法は、「技術の話」「微積分」を参照ください。) |
| |
| ∫f(x)dx (積分範囲aからb)= ∫f( g(t) ) dx/dt dt (積分範囲 ー1から1) |
| |
| したがって、-1<= t <= 1、x= g(t) = 0.5 (b-a) t + 0.5(b + a) で条件を満足するので、上の式は下記のように書けます。 |
| |
| ∫f(x)dx (積分範囲aからb)= 0.5 (b-a) ∫f(0.5 (b-a)t + 0.5(b+a) ) dt (積分範囲 ー1から1) |
| |
| これをガウス・ルジャンドルの数値積分の式に当てはめれば、次式が成り立ちます。 |
| |
 |
| |
| これで、任意の積分範囲 a<= x <= b の数値積分が得られました。n=4を想定して、誤差Rは省略しました。 |
| |
| |
| |
| Author : T. Oda |
| このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。 |