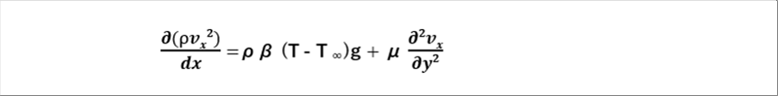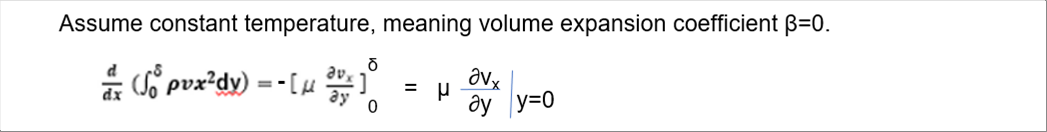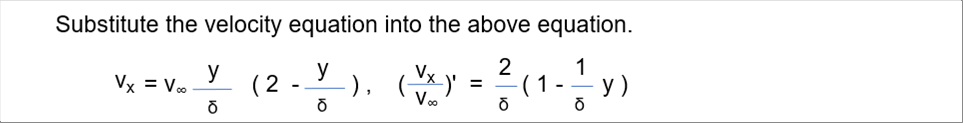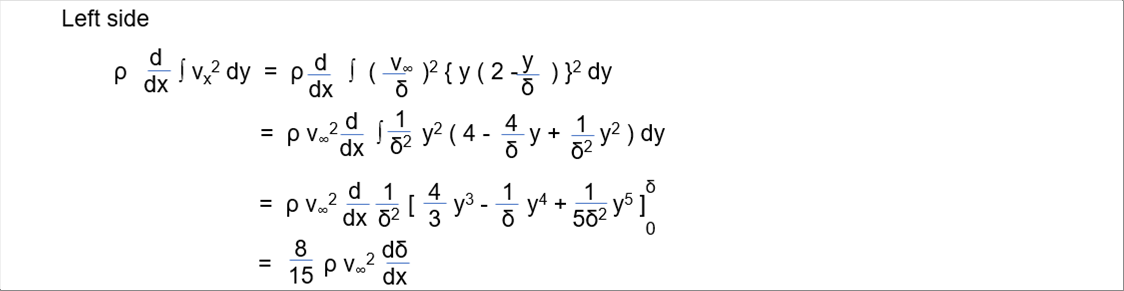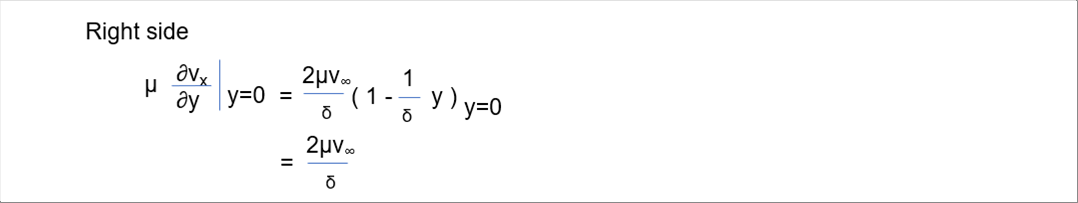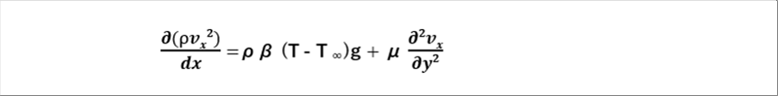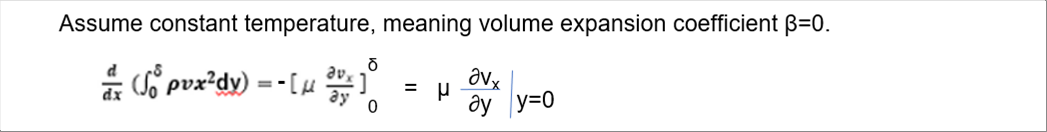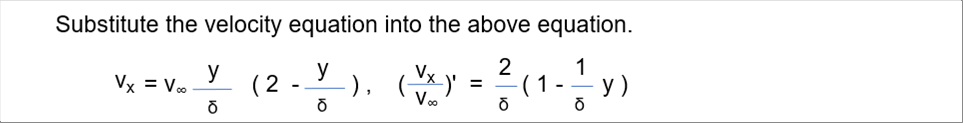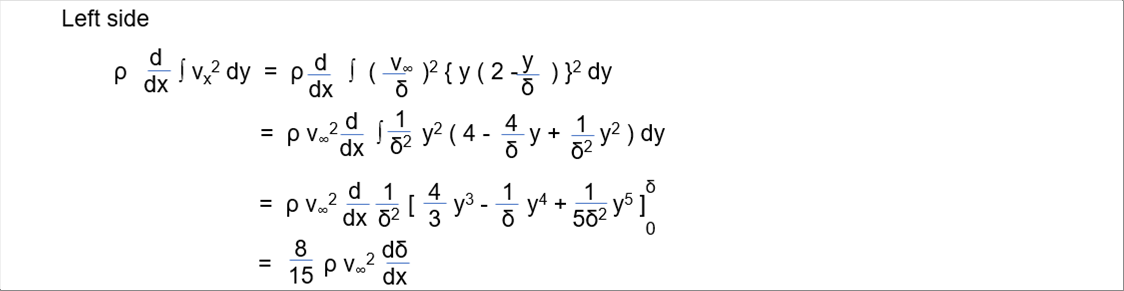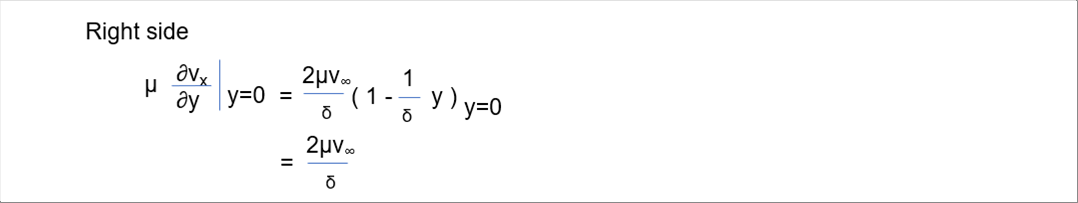| |
 |
| |
 |
| ● 粘性流体の境界層内速度と境界層厚さ |
| ● 非圧縮性流体のナビエ・ストークス方程式 |
| 〇 速度境界層 |
| ● 境界層内でのナビエストークスの方程式 |
| 〇 境界層内速度分布の計算 |
| 〇 境界層内ナビエ・ストークス積分方程式 |
| ● 実際の流体との違い |
| 〇 密度一定とした仮定の妥当性 |
| |
| |
 |
| ● 粘性流体の境界層内速度と境界層厚さ |
| |
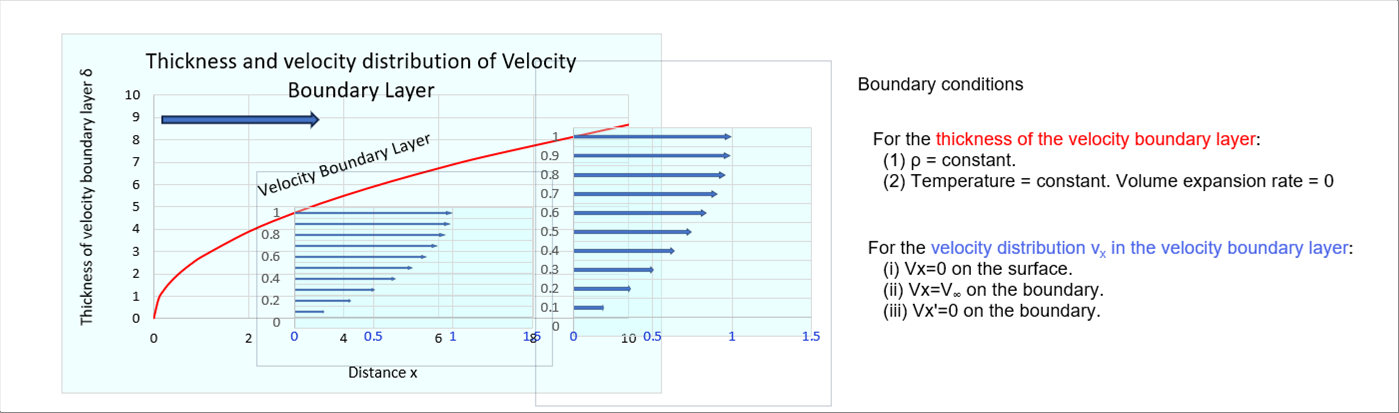
| 一定速度で流れる粘性流体の中にある静止物体の周りには、速度が遅い層「速度境界層」ができます。粘性流体の速度境界層厚さは、流れの後方に行くにしたがって厚くなります。また、速度分布は、物体表面ではゼロで、徐々に速くなり、境界層面で一定速度になります。 |
| |
 |
| |
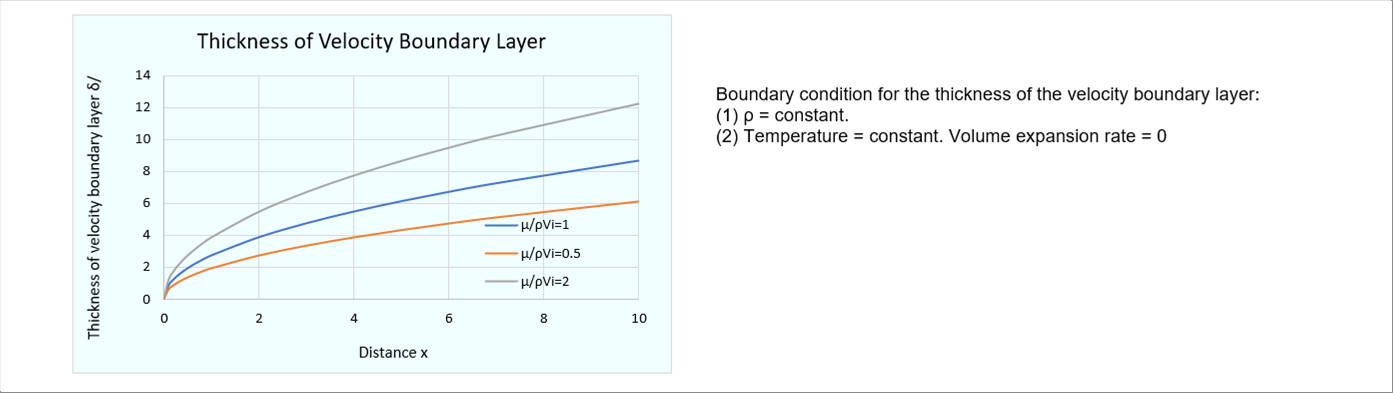
| 速度境界層厚さは、動粘度と一様流の速度の商のルートに比例します。 |
| |
 |
| |
 |
| ● 非圧縮性流体のナビエ・ストークス方程式 |
| |
| 未知数は速度と圧力で、円柱の周りの場合は未知数3(平面なので速度2成分、圧力1)です。適用する方程式は、非圧縮性流体のナビエ・ストークス方程式と連続の式です。ナビエ・ストークス方程式は成分ごとにあるので、方程式も3個になります。 |
| |
 |
| |
| したがって、未知数と方程式の数が同じなので(複素領域で)解けるはずですが、ナビエ・ストークス方程式の成分の式は複雑で、かつ、2階微分なので解析的には解けません。 |
| |
| 速度境界層内であれば、粘性の定義により物体表面では速度ゼロなどの条件があるので、速度境界層内での速度分布と、境界層厚さを解析的に解いてみます。 |
| |
| |
 |
| 〇 速度境界層 |
| |
| 一定速度の流体の中で物体が静止している場合、物体表面の流体速度は粘性によってゼロになります。表面からある距離離れるまで速度が遅い領域「速度境界層」が発生します。境界層では、一定速度になります。 |
| |
| 一般の流れでは乱流ですが、ここでは層流とします。また、はく離、渦は発生していないとします。 |
| |
 |
| ● 境界層内でのナビエストークスの方程式 |
| |
| 直交座標を用いた2次元ナビエ・ストークス方程式は、下のようになります。 |
| |
 |
| |
| この式の( )内を、微分の式を展開する際によく使う手法で計算を進めます。(詳細は微積分基礎を参照してください。) |
| |
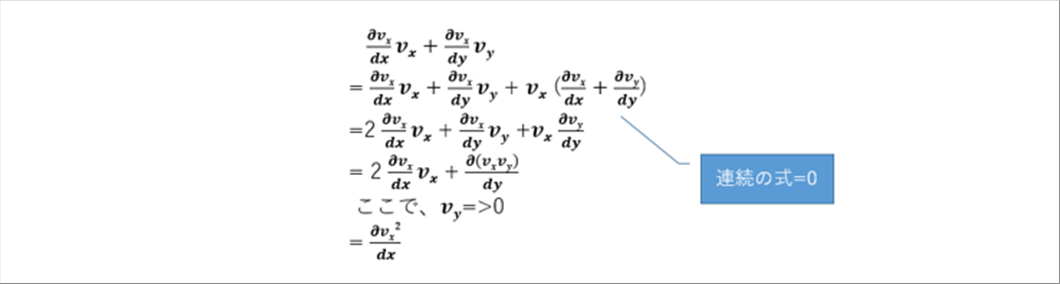 |
| ( )内は、x方向速度の2階微分となりました。 |
| |
| これをもとの方程式に戻すと、境界層内のナビエ・ストークス方程式は、次式で与えられます。 |
| |
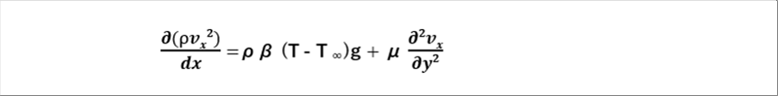 |
| |
 |
| 〇 境界層内速度分布の計算 |
| |
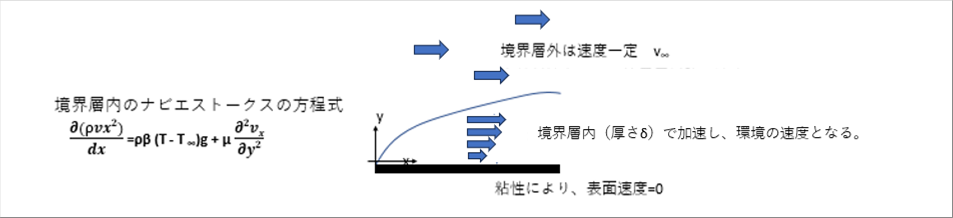
| 速度境界層の速度分布は、境界層内で加速し、境界で環境速度と同じになります。 |
| |
 |
| |
| 境界層内の位置xでの速度vxは、y軸方向で変化する。境界層内の速度分布は、上の左の絵のように、ゼロ、最大値、一定速度となります。表面近辺の速度変化は急で、境界層に近い部分の速度変化は小さいと想定すると、2次曲線で近似するのが妥当だと推測されます。 |
| |
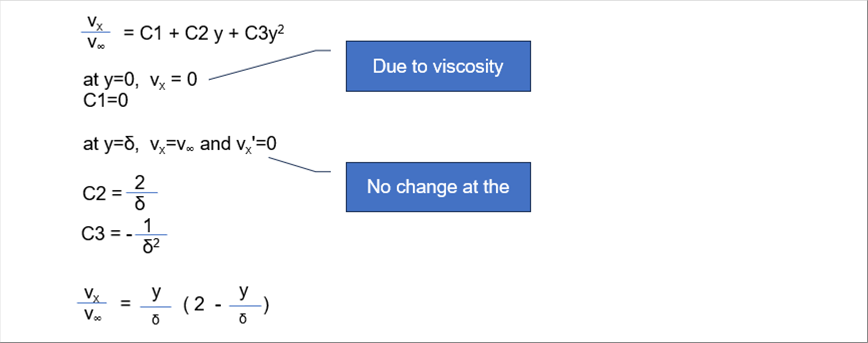
| VxとV∞の比で2次式を作ると、上の条件が満足できるので、2次式の定数項を特定するように考えていきます。境界条件として、次の3個があります。 |
| |
| (1) 粘性により、物体表面では速度ゼロ。 |
| |
| (2) 速度境界層での速度は、十分離れた位置の速度と同じ。 |
| |
| (3) 速度境界層での速度変化はゼロ。 |
| |
 |
| |
| 速度境界層内の速度分布の式が計算できました。境界層内の式なので、yはゼロからδまでです。また、この式は、速度と表面からの距離を、一定速度と境界層厚さでそれぞれ無次元化しているので、x方向のどの位置でも成立します。このホームページの最初のグラフはこの式を描きました。 |
| |
 |
| 〇 境界層内ナビエ・ストークス積分方程式 |
| |
| 次は、境界層厚みδを計算します。境界層内のナビエ・ストークス方程式を積分した式も成立します。 |
| |
 |
| |
| 温度が変化すると体積が膨張して浮力が発生します。熱伝達率の計算では重要な視点で、計算を続けていくと、ヌセルト数、グラスホフ数、プラントル数などが計算されます。ただし、ここでは温度を扱わないので、温度変化なし、体積膨張率=0とします。詳細は、熱力学を参照していただくとして、参考までに結論だけ書くと次式になります。 |
| |
 |
| |
| 本題に戻ります。体積膨張率=0の場合、境界層内のナビエ・ストークス方程式の積分は次の通りです。 |
| |
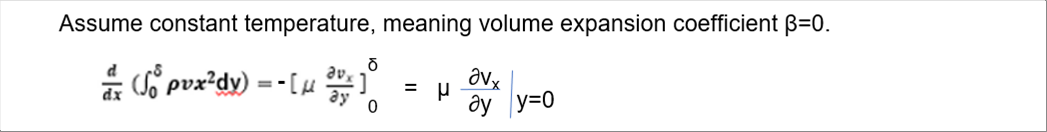 |
| |
| 境界層上の速度変化はゼロなので、物体表面の速度勾配だけが残ります。 |
| |
| 速度の式と微分をこの式に代入します。 |
| |
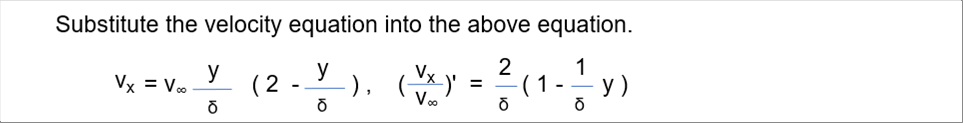 |
| |
| 左辺は以下となります。 |
| |
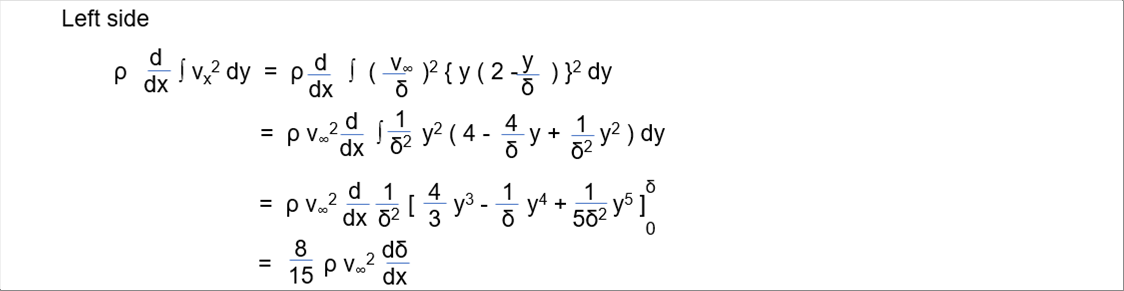 |
| |
| 右辺は次式となります。 |
| |
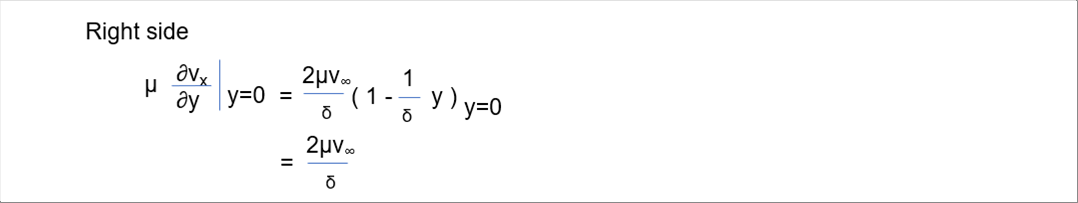 |
| |
| 境界層内ナビエ・ストークス積分方程式は、下のように整理できます。 |
| |
 |
| |
| 問題は初期値で、x=0の時の境界層厚みはどのくらいあるのかと、言うことになります。最初の模式図では流体と最初に接触するところの境界層厚みはゼロと想定しました。 |
| |
 |
| |
| この式から、境界層厚さは、次のことが言えます。 |
| |
| (1) 粘度が大きいほど境界層は厚い。 |
| |
| (2) 密度が大きいと境界層は薄い。 |
| |
| (3) 一様流の速度が速いと境界層は薄い。 |
| |
 |
| ● 実際の流体との違い |
| |
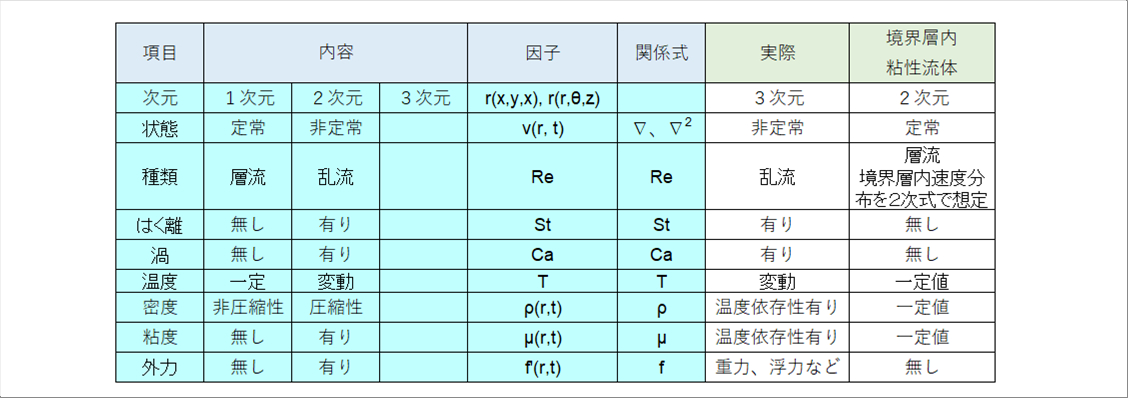
| 次の表は、計算をするために想定した内容と実際の流体を比較した示したものです。速度が遅い一様流に静止物を置いて十分時間が経って、ある断面を観察すると、2次元、定常流、層流、境界層内の速度分布、はく離と渦の発生まではほぼ問題ないと思われます。 |
| |
 |
| |
 |
| 〇 密度一定とした仮定の妥当性 |
| |
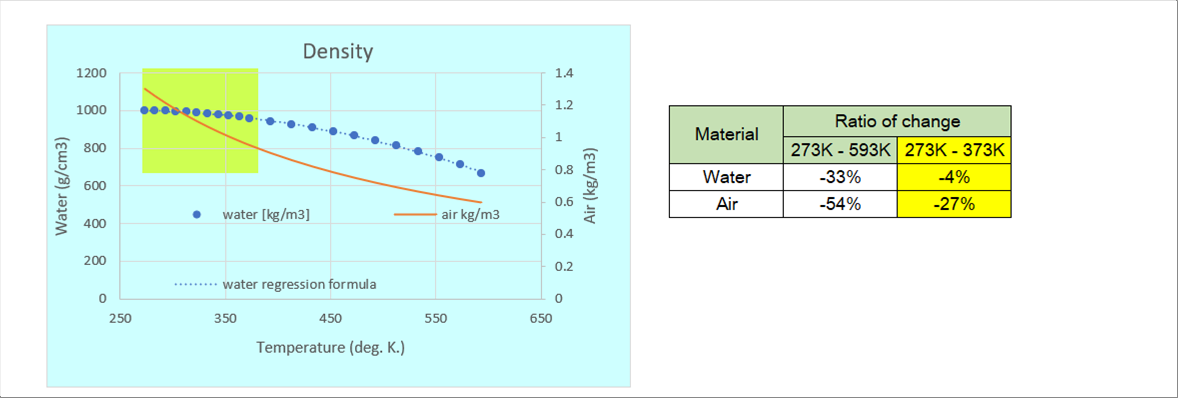
| このホームページでは、解析解を得るために温度一定としました。このため、体積膨張率はゼロ、密度と粘度は一定値とすることができました。この条件が妥当かどうかを見てみます。液体の代表である水は、大気圧下では273度Kから373度Kで液体です。(グラフのイエローの範囲)下のグラフは、273度Kから593度Cの水と空気の密度変化の比較です。 |
| |
 |
| |
| グラフの右の表は、水と空気の密度変化率です。イエローの範囲で空気の密度は27%変化しますが、水の変化率は4%です。この程度の変化率であれば、密度一定と仮定しても大きな問題ではないと思います。 |
| |
| |
| Author: T. Oda |
| このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。 |