| |
 |
| |
 |
| ● 生産現場の流体力学 |
| ● 流体力学は複雑です。 |
| ● 用語の定義と意味 |
| ー 粘度と動粘度 |
| ー 粘度と動粘度の温度の影響 |
| ー 高温での空気の粘度と動粘度 |
| ー レイノルズ数の定義と意味 |
| ー 層流と乱流 |
| |
 |
| ● 生産現場の流体力学 |
| |
| 家庭では、水道を使い、掃除機で掃除していると思います。自転車のタイヤ用のエアポンプや、家の壁や車の洗浄用に高圧洗浄機をお持ちの方も多いと思います。もっとほかのものもあると思いますが、すべて、空気と水を利用しています。 |
| |
| 生産現場では、家庭で使っているもののパワーアップ版を利用したり、それでも能力不足の場合は、ポンプを設置したりします。 |
| |
| 空気や水を流体といいますが、流体は自由に変形するため、変形させるための基礎知識は不要ですが、流体は動力や熱の伝達に使われるので、流体中に置かれた物体にかかる力などを知ることは興味深いと思われます。 |
| |
| 生産現場で扱っている流体は多岐にわたります。たとえば、気液を扱うクーラー、炉関連では燃料ガス、燃焼用空気、排気ガスなどです。生産設備で使われているものは、圧空、冷却水、作動油、潤滑油、スケール除去水、切削水、水圧試験機用水などです。 |
| |
| 設備やオペレーションの維持、管理、改善をする際に、簡単に実験、試験ができなかったり、試験結果の考察、解析に流体力学の基礎が役に立つので、流体力学の基礎を理解しておくのも意義があると思われます。 |
| |
 |
| ● 流体力学は複雑です。 |
| |
| 物体(固体)にかかる荷重は、机の上に置かれたリンゴなどの静荷重と、ホームランを打った時のような動荷重に大別されます。動荷重は、繰り返しかかる場合があり、さらに、ゼロからプラスなのか、マイナスからプラスなのかで、さらにいくつかに分類されます。釘打ちは、ゼロからプラス方向のみの繰り返し荷重、車のエンジンの振動などは、体が左右逆方向に振られるので、プラスとマイナスの繰り返し荷重だと思います。 |
| |
| 物体(固体)にかかる荷重がわかると、物体(固体)の運動方程式ができます。 |
| |
| 流体の運動は、流体にかかる荷重に加え、流体の性質と状態を考慮する必要があります。これが流体力学が複雑な理由です。 |
| |
| 流体の性質は、非圧縮性流体(液体)と、圧縮性流体(気体)の2種類です。流れの状態は、層流(低速)と乱流(高速)、ならびにその遷移領域の3種類です。運動の微分方程式は、性質と状態別に個別となり、全部を一度に表現した式はないと思います。(筆者の学生時代にはありませんでした。) |
| |
| 流体が空気の場合は、粘度、密度、比熱などの重要な指標に温度依存性があるため、さらに複雑になります。 |
| |
| 流体の運動方程式はナビエストークスの方程式で、別に紹介していますので、そちらを参照ください。ここでは、流体力学の基礎知識の整理と、いくつかの公式、実例を紹介したいと思います。 |
| |
| 流体力学を理解すると、流体の性質、流体にかかる力、流体が接触するものに及ぼす力とその動きなどがわかりますが、流体は自由に変形して複雑なので、運動の全部を解析的に解いた式は存在しないと思います 。 |
| |
| 家庭のガスコンロでケトルでお湯を沸かすなどが代表例になりますが、ガスコンロの炎の動きが流体の運動方程式で表され、炎の熱がケトル表面でケトルの伝達されるのは、熱力学の熱伝達方程式で表されるなど、流体力学と熱力学は深いかかわりがあります。 |
| |
 |
| ● 用語の定義と意味 |
| |
 |
| ー 粘度と動粘度 |
| |
| |
| 粘度と動粘度は、言葉から受ける感じが似ているため混同しがち(個人の感想)です。流体の動きや挙動を理解するのに重要なのでまとめました。 |
| |
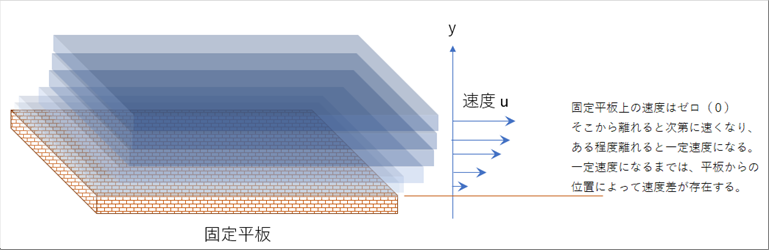
| 平板の上に流体が流れている状態を模式的に描くと下のようになります。 |
| |
 |
| |
| 平板上の流体の速度はゼロ、そこからy方向にはなれるにしたがって次第に速くなり、ある程度離れると一定速度になる。一定速度になるまでは、位置によって速度が違うので速度差が存在する。 |
| |
 |
| |
| 隣同士を考えると、速い層が遅い層を引っ張っている。(逆に、遅い層は速い層にブレーキをかけている。)この力がせん断力τと考えられる。つまり、τは速度差によって発生していると考えれられ、速度差に比例すると仮定し、この比例定数を粘度という。 |
| |
| ● 粘度μ:粘性係数とも。[Pa s パスカル秒]。 |
| |
| ● τ=μ du/dy 流体の速度勾配とせん断力の関係式 [ニュートンの粘性法則] |
| ● 流体中の力の伝わりやすさの指標。 |
| ● 粘度が大きいと、物体は動きにくいが、動いたことによる力は伝わりやすい。 |
| ● 流体中の物体の動きにくさの指標。 |
| |
| この比例定数ですが、流体で力を伝達する場合、適切な物質を選定する必要があります。同じ力を遠くまで伝える場合を考えてみます。液体の場合、水がせん断力を遠くまで伝えるには大きな速度が必要ですが、ペンキで同じ力を伝えようとする場合は、ずっと遅い速度でも伝えられます。気体では非常に顕著で、空気で同じ力を伝えようとしても、たぶん、不可能なレベルだと思われます。 |
| |
| 同じ速度差でも、空気、水、ペンキが伝えられる力が大きく違うのは、粘度に加え、密度も影響していると推測されます。密度が小さい流体よりも、密度が大きな流体のほうがより大きな力を伝達できると考えても差し支えないと思われます。 |
| |
| 粘度を密度で割ったものを、動粘度といいます。 |
| |
| ● 動粘度ν: [m2/s] |
| ● ν=μ/ρ (ρ:密度) |
| ● 粘度によってある距離離れた流体に力を伝える際に、密度が大きい流体は速度が小さくてもいい。密度が小さい流体は大きな速度が必要になる。 |
| ● 動粘度とは、流体の速度の伝わりやすさの指標といえる。 |
| ● 流体自体の動きにくさの指標。 |
| |
 |
| ー 粘度と動粘度の温度の影響 |
| |
| 流体を考えるうえで温度は重要なファクターになります。 |
| |
| 液体は日常でよく見かけるので温度の影響は体験していると思います。例えば、エンジンオイルは、温度が上がると粘度が下がることは車、バイクに乗っている方にはよくわかると思います。フライパンにサラダオイルを乗せて、温度を上げるとさらっと流れることもよく見られます。 |
| |
| 気体は、目に見えないものが多いので、温度が上がると粘度がどうなるか体感されている人は少ないと思いますが、液体と逆で、粘度が大きくなります。さらに、気体で忘れてはいけないことは温度が上がると体積が増えることです。この影響で、温度が上がると気体の密度は小さくなります。この密度変化は動粘度に大きな影響を与えます。 |
| |
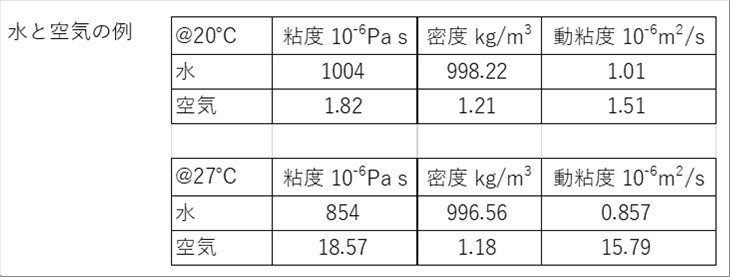
| 水と空気の温度摂氏20度の場合と27度の場合の比較は下の通りです。27度では、空気の密度は大きく変化しませんが、粘度が10倍程度になっているのがわかると思います。 |
| |
 |
| |
| |
 |
| ー 高温での空気の粘度と動粘度 |
| |
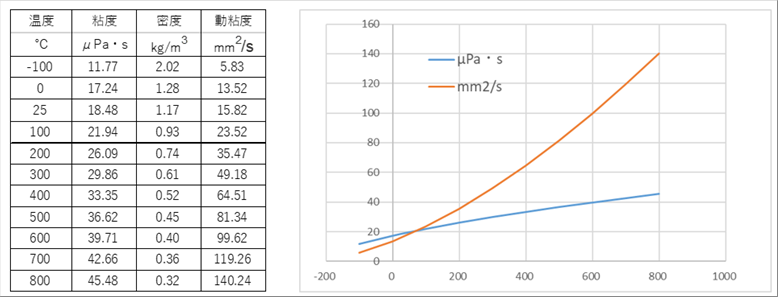
| 大気圧での空気の粘度と動粘度は次のようになっているそうです。 |
| |
| グラフを右につけましたが、空気の粘度と動粘度は温度によって大きく変わることがわかります。シミュレーションをする場合など、適切な数値を使うか、回帰式を利用するのが適切だと思われます。 |
| |
 |
| |
 |
| ー レイノルズ数の定義と意味 |
| |
| レイノルズ数は流体力学で重要な指標の一つです。レイノルズ数の数値によって流れの様相が変わるので、適用する式が変わったりします。 |
| |
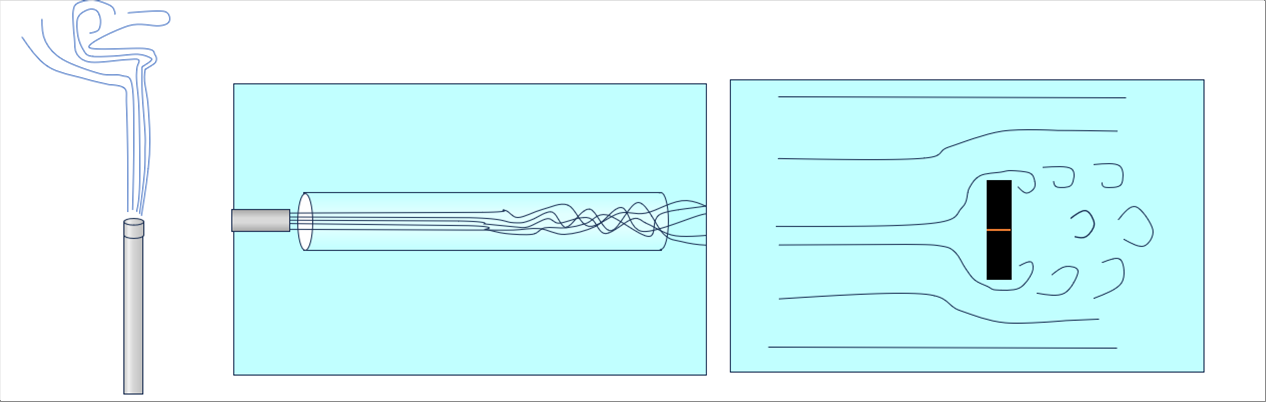
| 川がゆっくり流れているときは、川の流れはスムーズに見えます。流れが速くなると、荒れ狂っているように見えます。 |
| |
 |
| |
| また、同じ速さでも、流れる距離が長くなると、下流に行くに従い、ところどころが荒れているように見えます。 |
| |
 |
| |
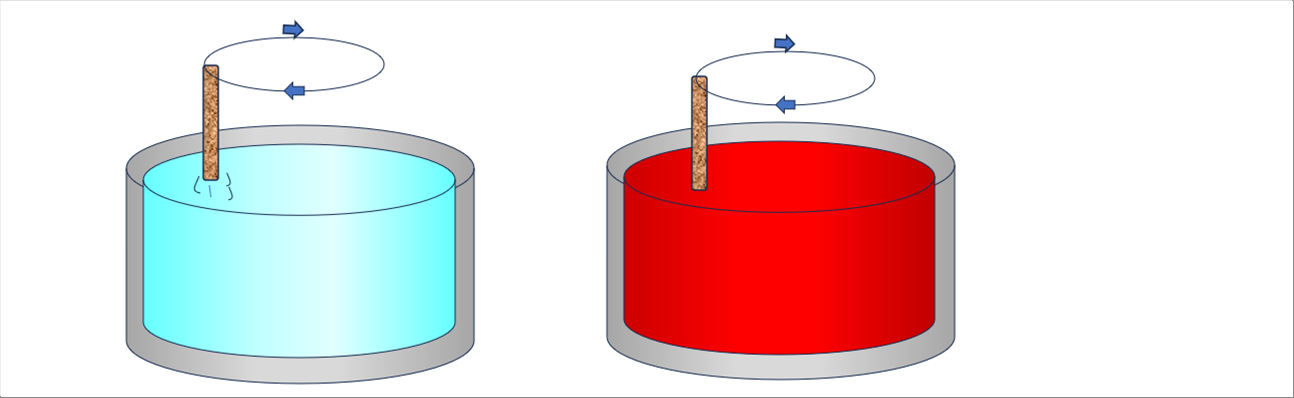
| へらを使って水を撹拌する場合とペンキを撹拌する場合では、水のほうが同じ速さでも荒れた流れに見えます。 |
| |
 |
| |
| このように、流れの状態は、速度、粘度、動粘度のほかに、流路の長さ、幅などの寸法の影響があると思われます。我々の大先輩である、19世紀のストークスさん、レイノルズさんなどが提唱された数字がレイノルズ数です。 |
| |
| ● 粘性が流れに及ぼす影響度の指標 [無次元量] |
| ● 慣性力ρU^2と粘性力μU/Dの比率 |
 |
| U:流れの代表速度、 |
| L;流れの代表長さ、D:パイプ内の流れはパイプ内径を代表長さにとる。 |
| ν:動粘度、μ:粘度 |
| |
| ● 意味合い |
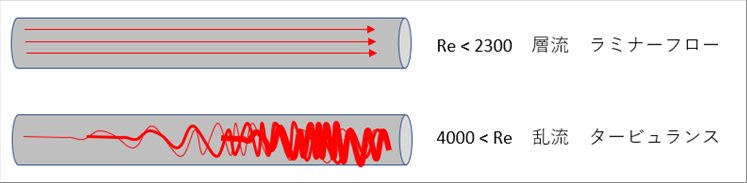
| ● レイノルズ数が小さい:粘性の影響で層流となる。 |
| ● レイノルズ数が大きい:慣性力が支配的となり乱流となる。 |
| |
 |
| |
 |
| ー 層流と乱流 |
| |
| 層流と乱流は、見た目だけでなく、状態と速度において、大きな違いがあります。層流は定常流で、壁面からの距離の関数で速度が記述できます。乱流は、速度変化が距離の関数になるとは限りません。層流の流れの分布は、中央で最大値、壁面で壁面との相対速度ゼロとなりますが、乱流の流れ分布は端部で最大になり、中央部では小さくなります。層流と乱流の中間状態もあり、遷移状態といわれています。 |
| |
| 家庭内、製造現場などで見られる空気や水の流れは、恣意的に層流としてない限りは、通常は乱流となっていると考えられます。例えば、自転車で、ある程度早くなると衣服がはためきますが、これは、自分の周りに空気の渦ができているからです。一般的に、何かを「能率的に」実行する場合、速い速度で処理することが基本になると思われますが、空気や水を速く動かすと乱流になります。 |
| |
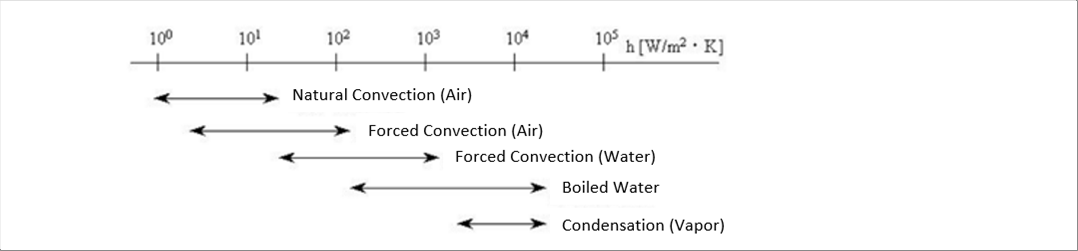
| 流体を利用して熱を伝達することを熱伝達といいますが、乱流の熱伝達係数は層流の熱伝達係数より非常に大きくなっています。これは、乱流だと運動量の交換が盛んにおこなわれるためです。(熱伝達係数は、「熱伝達」を参照してください。) |
| |
 |
| |
| 流体の運動は下の「ナビエ・ストークス方程式」で記述できます。導出方法は「ナビエ・ストークス方程式の導出」で紹介しているので参照してください。ナビエ・ストークス方程式を定常流として解くと層流の解が得られ、非定常流として解くと乱流の解が得られます。ただし、この方程式は、例外的に特別な場合を除き解析的には解けないので、数値計算が必須です。定常解は、ラップトップパソコンで十分計算可能ですが、乱流の解析結果を得るためには、高性能の計算機が必要になります。 |
| |
 |
| |
| このホームページでは、高性能な計算機での専門的な数値計算はできませんので、乱流は割愛させていただきます。数値解析の例として、ラップトップでパイプの温度計算をした例を「数値解析」に載せてありますので、参考にして下さい。 |
| |
| Author: T. Oda |
| このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。 |









































