| |
 |
| |
 |
| ● 圧力損失計算方法と演習 |
| 〇 演習 ベルヌイの定理 |
| 〇 圧力損失 |
| (1) 計算手順1 レイノルズ数の計算 |
| (2) 手順2 管摩擦係数の計算 ムーディー線図、計算式 |
| (3) 手順3 圧力損失の計算 |
| (4) 手順3−1a 管摩擦係数 ムーディー線図 |
| (5) 手順3−1b 管摩擦係数 ファニングの式 |
| 〇 注意 二つの摩擦係数 ダルシーの式 |
| (6) 手順3−2a 圧力損失係数 直管部分 |
| (7) 手順3−2b 圧力損失エルボー、T、仕切弁 |
| (8) 圧力損失計算例 |
| ● 圧力損失係数 |
| 〇 タンクから配管への入口 |
| 〇 配管断面積、角度変化 |
| 〇 全開玉型弁(グローブバルブ) |
| 〇 仕切弁の開度 |
| 〇 配管の分岐 |
| |
| |
| |
 |
| ● 圧力損失計算方法と演習 |
 |
| 〇 演習 ベルヌイの定理 |
| |
 |
| |
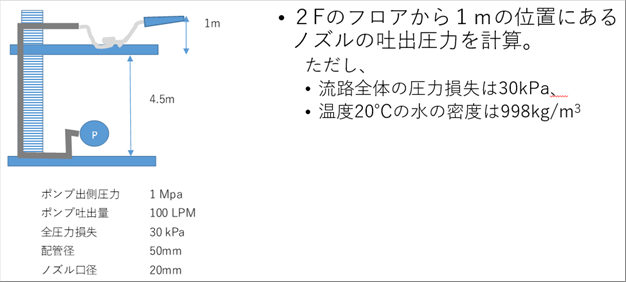
| ポンプが1Fにあり、2Fのフロアからノズルで吐出する場合の圧力を計算する。ノズルは腰の高さあたりにあるとすれば、2Fのフロアから1m程度の位置と推定される。 |
| |
| ポイント1をポンプ位置、ポイント2をノズル位置とすれば、圧力損失のあるベルヌイの定理を使って吐出圧力が計算できる。ポンプのスペックは左下にあり、流路の圧力損失と水の密度が記載されているので、淡々と計算すれば計算でき、0.78MPaとなる。 |
| |
| 計算で注意することは、単位をそろえることで、ポンプスペックは吐出量は毎分100リットル、ポンプ出側圧力がメガパスカル、圧力損失がキロパスカル、配管とノズルがミリメートル、密度が立方メートルなので、同じ単位系に変換してから計算する。 |
| |
 |
| 〇 圧力損失 |
| |
| このように、圧力損失がわかれば、ほかの数値は簡単な計算で得ることができるが、圧力損失がわかっていることは、上のような演習以外ではほとんどない。(と、思います。)実測するのがもっとも正確ですが、材料力学と同様、物を作る前に知りたいというのが大前提になります。 |
| |
| 材料力学では、ヤング率、断面二次モーメントなどで事前に知りたいことが計算できますが、流体力学では、流れの様子がレイノルズ数で変わるという厄介な問題があります。(個人的な意見です。) |
| |
| 圧力損失を計算する手順は、まずレイノルズ数を計算し、流路はパイプの場合が多いので、管摩擦係数を計算します。最後に、圧力損失を計算します。専門の会社様などではもっと近代的な方法をとられていると思いますが、自分で計算してみようという場合には、若干手間ですが、こういう方法で計算できるという紹介です。 |
| |
 |
| (1) 計算手順1 レイノルズ数の計算 |
| |
| ● レイノルズ数計算 |
| ● 流体の流速計算 |
| ● 密度計算 |
| ● 物性表は、気体は標準状態の数値で表記されている。101.3kPa, 0℃,0.0224m3/mol |
| ● 温度補正 気体ρ=m*(101.3+P)*273/(0.0224*1000*101.3*(273+T)) |
| ● mモル質量[g/mol], P[kPaG],T[deg. C] |
| ● 粘度を調べる。 |
| ● Reを計算する。 |
| |
 |
| (2) 手順2 管摩擦係数の計算 ムーディー線図、計算式 |
| |
| 管摩擦係数を計算する。 |
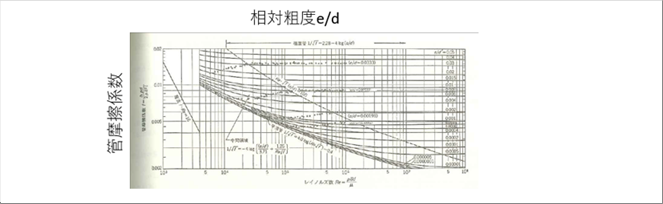
| ● ムーディー線図か計算式を使って管摩擦係数を求めます。ムーディー線図は下のようなグラフで、読み方は手順3−1aで説明します。 |
| |
 |
| |
 |
| (3) 手順3 圧力損失の計算 |
| |
| ● エルボーなどの相当長さを計算し、総配管長を求めファニングの式を使う。A |
| ● 入口部、急縮小部、急拡大部、配管出口の圧力損失を計算する。B |
| ● 圧力損失 = A +B |
| |
 |
| (4) 手順3−1a 管摩擦係数 ムーディー線図 |
| |
| ● ムーディー線図 |
| |
| ムーディー線図は、レイノルズ数と相対粗度e/dから、管摩擦係数を読み取るものです。相当広い範囲を網羅している線図なので、汎用性があるとも言えますが、正直言って、読み取るのは困難です。通常は、ムーディー線図にある範囲より狭い範囲を知りたいと思いますので、その条件に合った実験式を作って使うのがいいと思います。 |
| |
| 管内面の粗さはレイノルズ数に大きな影響を与えます。ムーディー線図は相対値をつかっているので無次元化されていて広い範囲の材質を網羅しているといえますが、同上の理由で広すぎると思います。(個人の意見です。) |
| |
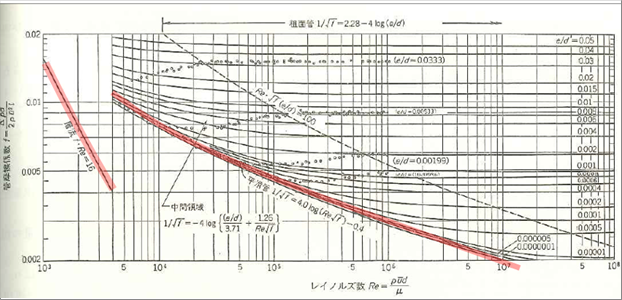
| 相対粗度の計算は、使う予定の材質の粗度(mm)を計測するのが一番ですが、目安として下のような表を使っても大きな影響はないと思います。 |
| |
 |
 |
| |
 |
| (5) 手順3−1b 管摩擦係数 ファニングの式 |
| |
| ファニングの摩擦係数 f の式は、次のように導出できます。 |
| |
 |
| |
| ● 層流(Re<=3000) 内壁の粗さによらず f=16/Re |
| ● 遷移領域 割愛させていただきます。 |
| ● 乱流、平滑管(3000
|
| ● 乱流 粗い管 (3000
|
| |
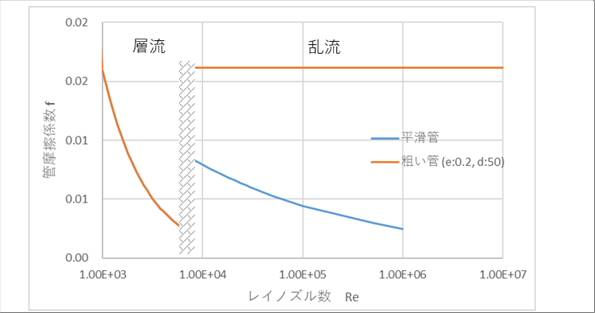
| 摩擦係数を考えるうえで内面粗度は気になりますが、層流の摩擦係数は粗さによらずレイノルズ数だけで決まり、乱流は平滑管と粗い管の2式だけなので、あまり気にする必要はないのかもしれません。 |
| |
 |
| |
| 一つのグラフにすると上のようになります。層流と乱流で式が連続になっていないのでその部分は波パターンにしています。シミュレーションや計算をする場合は、レイノルズ数が遷移領域になったら、どちらかの数値を使っておいて差し支えないと思いますが、レイノルズ数が遷移範囲にならないようにするのがベストだと思います。 |
| |
 |
| 〇 注意 二つの摩擦係数 ダルシーの式 |
| |
| ベルヌイの定理の水頭で、圧力損失水頭 hf をあらわすと次式となります。 λは、ダルシーの摩擦係数と呼ばれています。 |
| |
 |
| |
| ダルシーの摩擦係数 λ は、ファニングの式の摩擦係数 f の4倍になります。TSコンサルティングのホームページでは、混同しないようにfとλを使用していますが、どちらも「摩擦係数」と表記します。ムーディー線図で摩擦係数を読むときも、どちらの摩擦係数がy軸なのか、注意が必要です。圧力損失を計算する場合、fは4倍しますが、λはそのまま使います。 |
| |
 |
| (6) 手順3−2a 圧力損失係数 直管部分 |
| |
| ● 圧力損失係数 直管部分 |
| |
| 摩擦係数が決まったら、速度、配管長さ、内径などで圧力損失が計算できます。流路が曲がっていたり、バルブがあったりするとそれ以上の圧力損失が発生しますが、これらは直管の長さ補正をすることで圧力損失を計算するので、直管部分の圧力損失の計算が重要になります。 |
| |
| ● 直管部分の圧損 |
| |
 |
| f:管摩擦係数、λ管摩擦係数、v:流体の速度[m/s]、ρ:密度[kg/m3]、L:配管長[m]、D:配管径[m] |
| |
 |
| (7) 手順3−2b 圧力損失エルボー、T、仕切弁 |
| |
| 形状に応じて管長Lの替わりに、換算した相当長さを使う。 |
 |
| 相当長さ係数 n=Ln/D |
| 45度エルボー:15、90度エルボー:15-32、 |
| T字管:40-90、 |
| ゲート弁 全開:1-7, 3/4開:40, 1/2開:200, 1/4開:800 |
| |
 |
| (8) 圧力損失計算例 |
| |
 |
| |
| 計算 |
| ● Re=54.1*10^(-3)*1.2*1000/( 0.797*10^(-3) ) = 81455 乱流 |
| ● f = 0.0791*Re^(-0.25)=4.682*10^(-3) |
| ● 圧力損失 |
| ● 90度エルボ換算長 15*54.1mm*6 = 4.9 m |
| ● Ts 換算長 80*54.1mmX2 = 8.7 m |
| ● 配管長 L = 100+4.9+8.7 = 113.6 |
| ● ΔPL=4f x 0.5ρv^2 *L/D = 28.32 [kPa] |
| |
 |
| ● 圧力損失係数 |
| |
| 各種圧力損失係数がたくさん提供されているので、いくつかピックアップしてみました。参考にしたホームページは以下の通りです。 |
| |
| クリックした際に詐欺サイトに誘導される場合があるので、グラフィックで貼り付けさせていただきます。(TSコンサルティングのメニューの内部リンクはフィッシング詐欺対策としてタブナビング対応をしています。) |
| |
 |
| |
 |
| 〇 タンクから配管への入口 |
| |
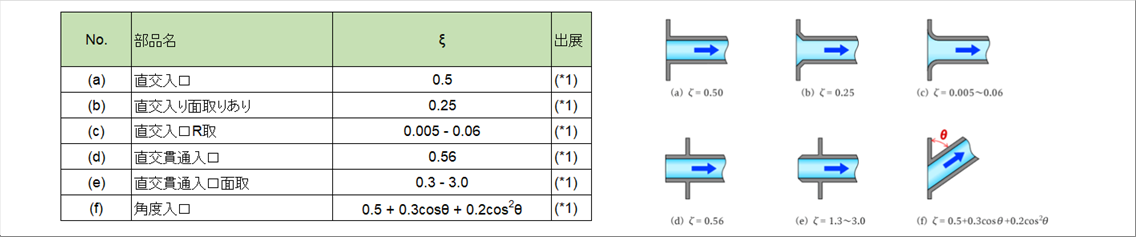 |
| |
 |
| 〇 配管断面積、角度変化 |
| |
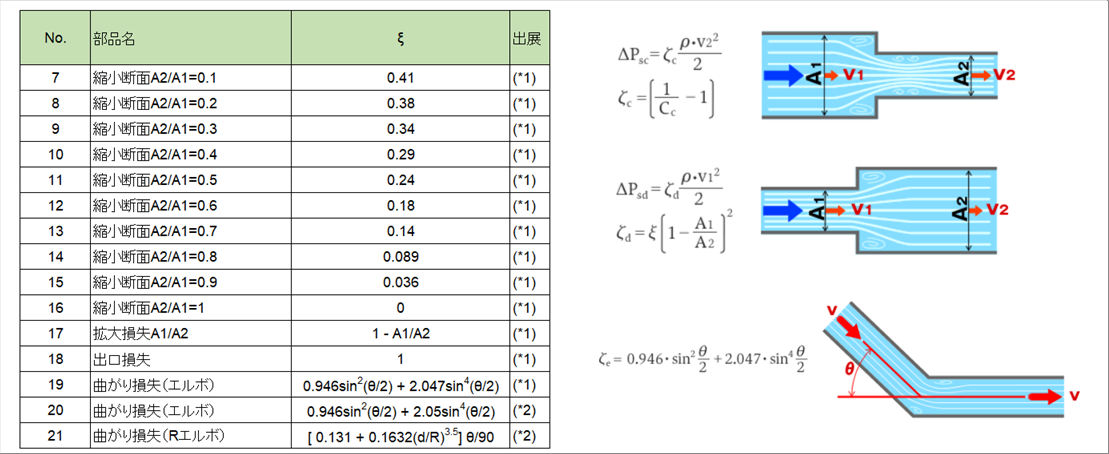 |
| |
 |
| 〇 全開玉型弁(グローブバルブ) |
| |
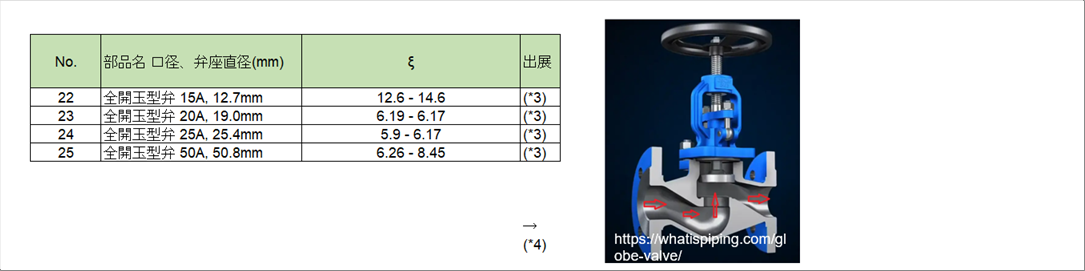 |
| |
 |
| 〇 仕切弁の開度 |
| |
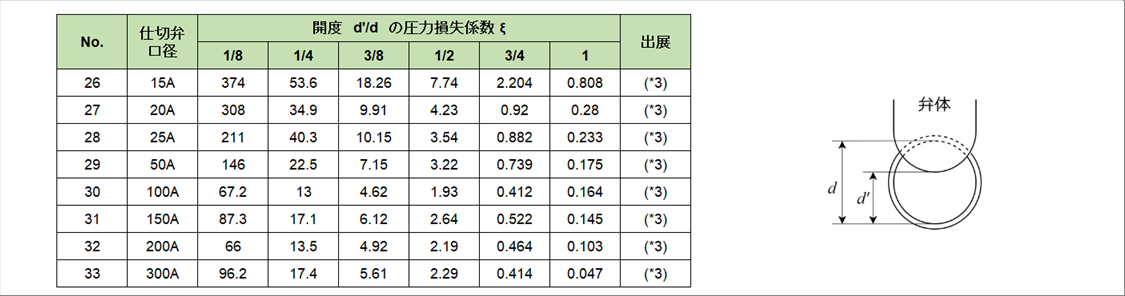 |
| |
 |
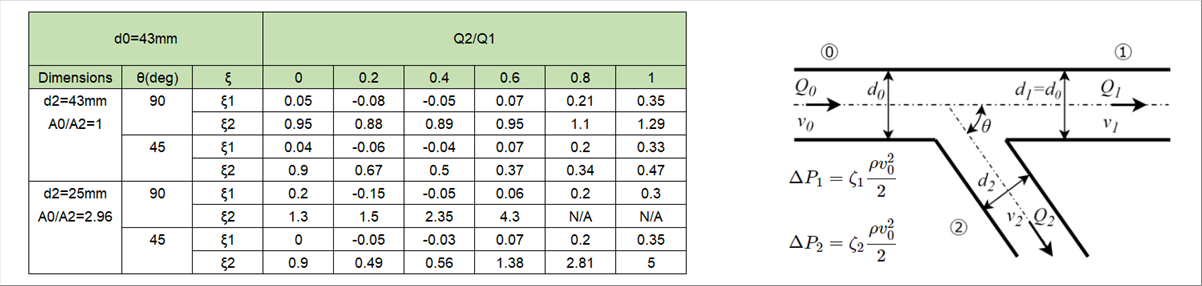
| 〇 配管の分岐 |
| |
 |
| |
| |
| Author: T. Oda |
| このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。 |







































































