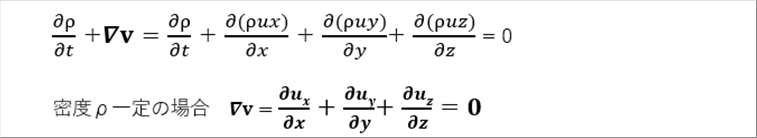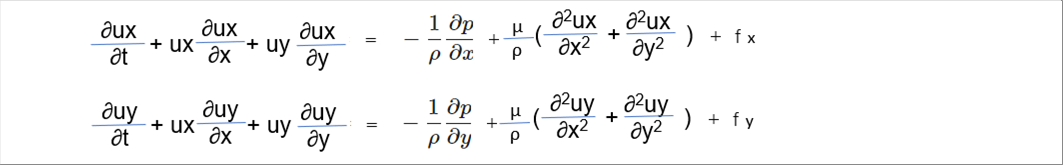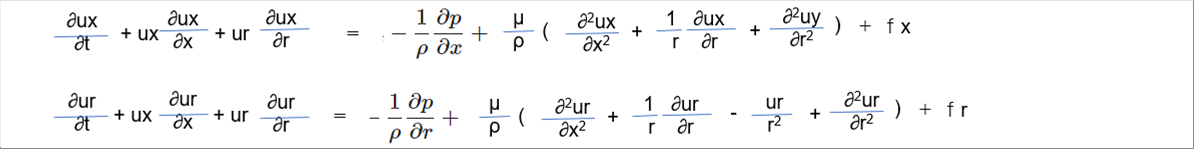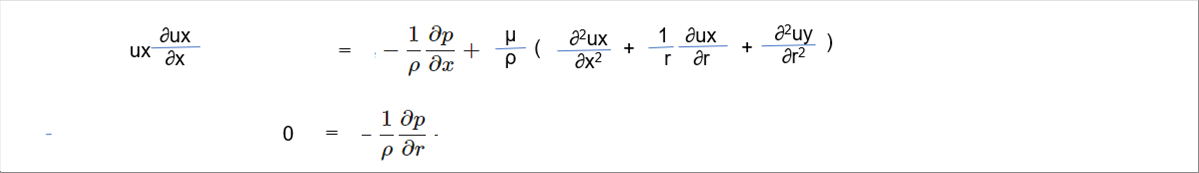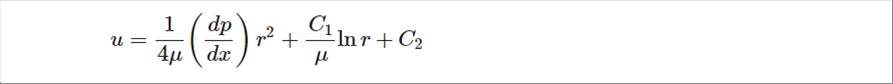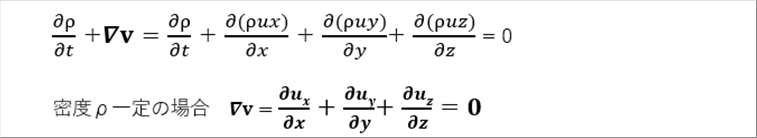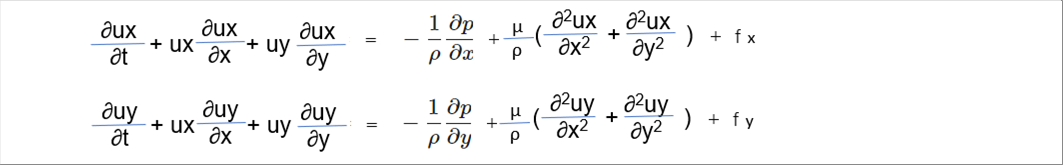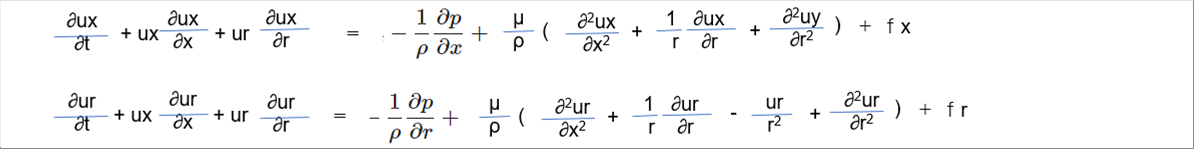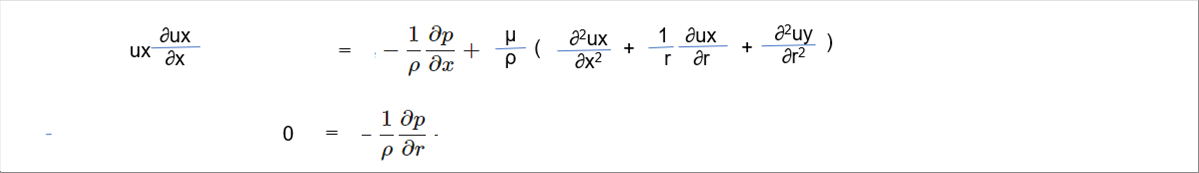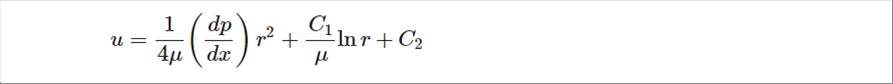並行平板、円管内流れ　Flow in Parallel Plates and in a Cylinder
●　流体の運動の記述
●　流体の運動方程式と解法
〇　オイラー方程式
〇　ナビエストークス方程式
〇　連続の式
〇　並行平板間の流れ
〇　円管内の流れ
〇　最大速度、平均速度、流量
〇　圧力損失
●　流体の運動の記述
流体の運動を記述する式は、理想気体の状態方程式、連続の式、運動方程式とエネルギーの式があります。
方程式の数は、それぞれ１個、１個、３個、１個で、合計６個の式があります。
未知数は、圧力、密度、速度、温度で、それぞれ１個、１個、３個、１個で、合計６個です。
したがって、これらを連立させれば解けます。
ただし、流体の運動方程式はナビエストークス方程式と言い、複雑かつ非線形2階偏微分方程式なので、解析的に解いたものはない。（と思います。）通常は、いくつかの仮定を置いて数値解析で解を得ます。
ここでは、さらにいくつか仮定をおいて、並行平板間の流れの速度分布と、パイプ内面の速度分布を計算します。
●　流体の運動方程式と解法
●　オイラー方程式
流体力学の基礎方程式は３個の保存則で、質量保存則、運動量保存則、エネルギー保存則です。エネルギー保存則は、「ベルヌイの定理」で説明しましたので詳細はそちらを参照ください。
非粘性流体（完全流体）の運動方程式は、オイラー方程式 (Euler Equation) といいます。ここでは、工場などで扱う流体力学を考えていますので、粘性項は無視できないと思います。したがって、オイラー方程式は割愛させていただきます。
オイラー方程式は、粘性を考慮したナビエストークス方程式(Navie Stokes Equation)から、粘性項を除いた式なので、オイラー方程式に興味がある方は、ナビエストークス方程式を見ていく際に粘性項をカットしながら見ていただくといいと思います。
〇　ナビエストークス方程式
流体の運動に関係するのは、流体の密度、流入量、流出量、粘性、内部圧力、外力などで、それらを一度に表現したものがナビエストークスの方程式です。
ナビエストークスの方程式は、３次元流の運動方程式で、座標軸ごとに書いていくととてつもなく長くなります。プログラムを組むときには必要になりますが、読んでいくときには似たような記述を何度も見ることになります。（きっとミスタイプも多くなると思います。。。。）
ナビエストークス方程式は、次式で与えられます。
この式は、場所ｒと時間ｔで変化する流体の速度は、流体にかかる圧力ｐ、流体の粘性μ、外力ｆによってきまることを示しています。
記号∇と?は見たことのない人もいるかもしれませんが、それぞれナブラ、ラプラシアンと読み、一階微分和、二階微分和を表現しているので、見やすい式にまとめられます。
ナブラは、直交座標系での３項を1項で表現でき、ラプラシアンは、9項を1項で表現していることがわかると思います。
また、これらの演算子を使えば、極座標系でも同じ表現になります。
〇　連続の式
連続の式は、次式で与えられます。
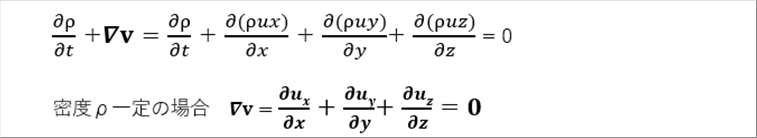流体が連続しているということは、流体が集まってくれば密度が上がり、逃げていけば密度が薄くなるということです。これなら、流体が切れて真空の場所ができたりしません。密度一定の場合は、各速度成分の変化率を足してゼロになります。
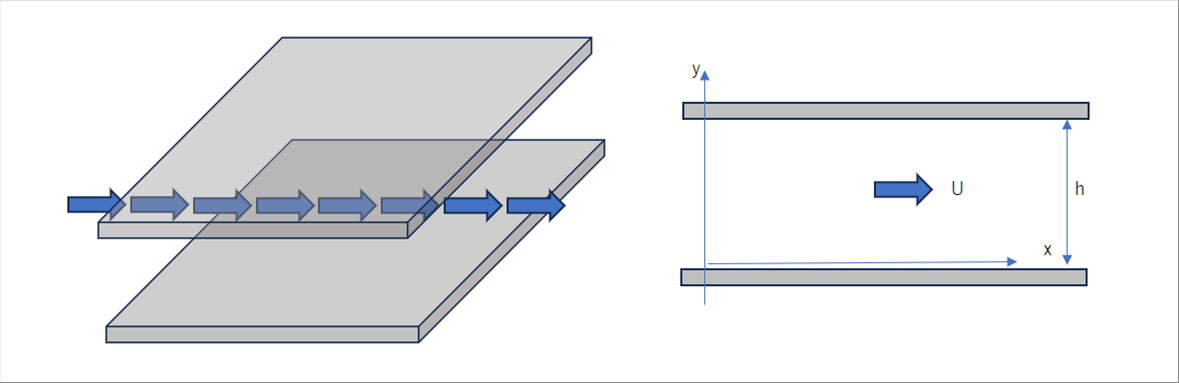
〇　並行平板間の流れ
非圧縮性のナビエストークス方程式は、３次元では解析的に解くことは非常に困難です。平行平板が十分に幅がある場合の、中央部分の層流流れを想定して計算してみたいと思います。
この場合、ｚ方向の流れはないと想定できるので、ｘ、ｙ２次元のナビエストークス方程式と連続の式の連立方程式を解きます。
両辺を密度で割ってナビエストークス方程式をｘ方向、ｙ方向に分けて書くと、次のようになります。
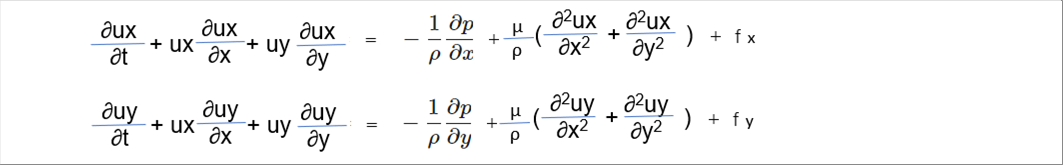定常流なので、時間項はゼロ、並行流なので、uy = 0 です。連続の式より、次式が得られます。
さらに、外力がかかっていない場合は、ｆ＝０なので、ナビエストークス方程式は次の２式で与えられます。（外力には重力も含まれますが、ない場合を考えます。）
ｙ方向の式（下の式）より、ｙ方向のｐ変化はないことがわかります。したがって、ｐはｘだけの関数であることがわかります。
上の式を整理して、次式が得られます。
この微分方程式は積分できます。ｙについて2回積分すると、次式が得られます。
平行平板が静止している場合は、両平板の内側で速度ゼロになります。 y=0, h で ux = 0。 定数は、次式で与えられます。
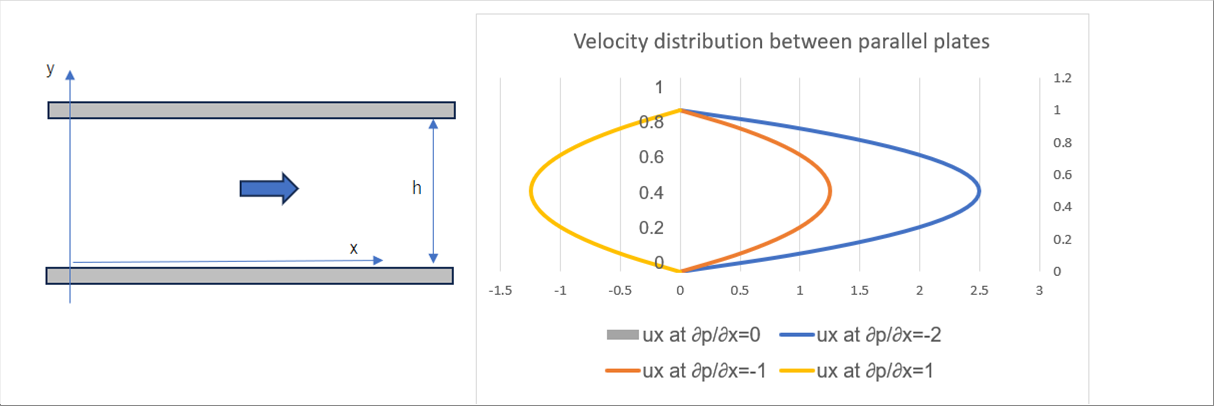
速度分布 ux は、壁面からの距離 y の２乗の関数になることがわかります。圧力 p の変化率をー２、ー１、０，１で計算した結果は次のグラフのようになります。
進行方向が負圧になると右に流れ、正圧になると左に流れることがわかります。
なお、この流れの平均速度は、最大速度の半分になります。計算方法などは、次の「円管内の流れ」を参照してください。
〇　円管内の流れ
次に、円管（パイプ）内の流れを考えてみたいと思います。
平行平板の時と同様、ナビエストークス方程式は以下で与えられます。
円管（パイプ）内の場合、円柱座標を使うのが便利です。ナビエストークス方程式のナブラとラプラシアンを円柱座標で表すと次式となります。ナブラ、ラプラシアンの円柱座標での詳細は、熱力学（ｒ、θ、ｚ）を参照してください。その際、ｚをｘに、かつ、熱量を流量と読み替えていただければ、そのまま使えます。
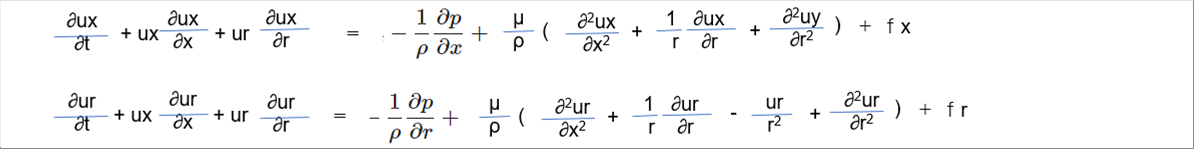平行平板の時と同様、定常流、外力ｆ（重力含む）はゼロ、断面積一定、粘度一定、ｒ方向流れ、θ方向流れはないとします。
時間項 = 0, fx = fy = 0, ur = 0 の条件から、次式が得られます。
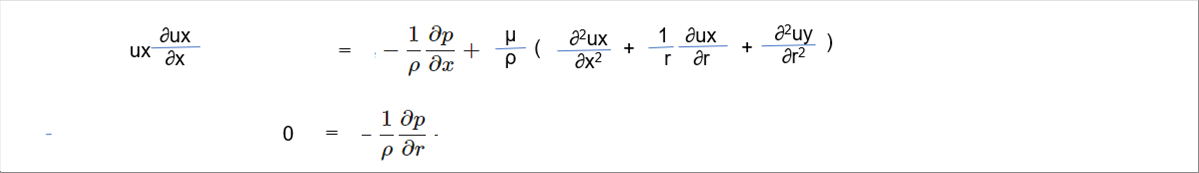下の式より、半径方向の圧力変化はないので、ｐはｘだけの関数です。（p=p(x) となります。）
速度は、ｘ方向には変化しないので、uxのx方向１階微分、２階微分はゼロです。
これらを上の式に代入すると次式となります。
この式をｒで２回積分して、次式が得られます。（分数の積分は、「微積分」を参照ください。）
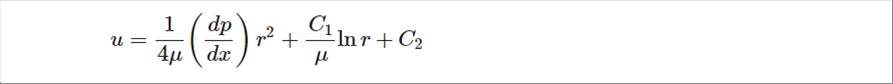並行平板の時と同様、C1とC2を決定します。まず、C1を考えてみたいと思います。円柱座標系のナビエストークス方程式は、ｒが分母にあるため、中心部は特異点で、ｒ＝０では定義できません。いろいろな簡略化をして解いた上の式の２項目は対数で、ｒ＝０は定義できません。（exp(x)=0のｘは定義できません。）実際の速度は有限な値なので、Ｃ１=0です。
次にC2ですが、流体の粘性のため、円管（パイプ）内壁面での速度 u = 0です。この条件よりC2は決定できて、速度は次式で与えられます。
円管（パイプ）内直径を１、圧力勾配ー２，ー１，０，１の場合の管内流速分布を計算した結果を下に示します。
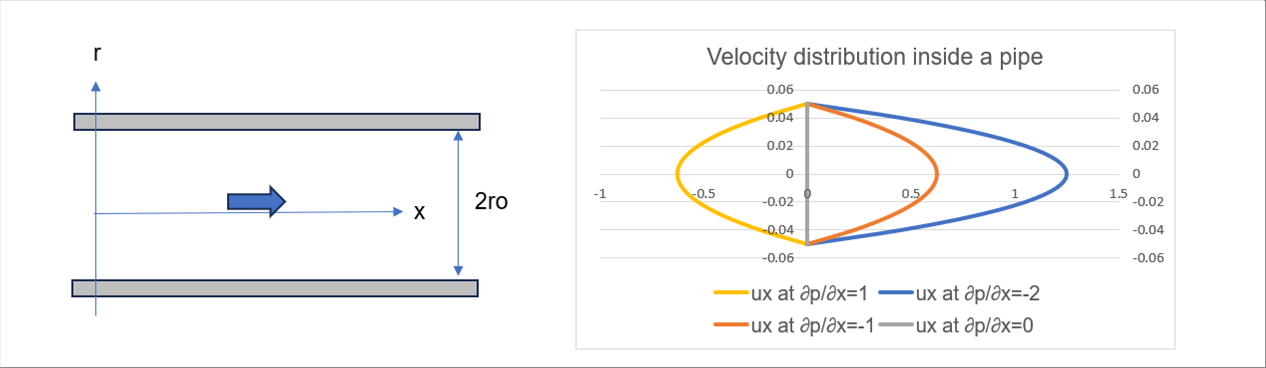並行平板の流れと同様に、進行方向が負圧だと右に流れ、正圧だと左に流れます。圧力勾配がないと流れません。
〇　最大速度、平均速度、流量
並行平板の間を流れる流体の速度計算は、流れの紹介のために使ったので、計算方法を割愛しましたが、パイプは配管などの計算に使えるので、計算方法を紹介します。
円管（パイプ）内速度分布の速度は、中心部で最大速度になります。最大速度は、速度の式にｒ＝０を代入して求めます。管内の流量は、速度を半径方向に積分して求められます。また、平均速度は、流量を断面積で除して求めます。
上の式より、次のことが言えます。
１）最大速度、平均速度、流量は、圧力勾配に比例する。
２）平均流速は、最大速度の半分になる。
３）平均流速、最大流速は内径の２乗に比例し、流量は内径の４乗に比例する。
〇　圧力損失
圧力損失は、圧力勾配と配管長の乗算で求められます。
圧力損失は、配管長と流速（平均流速、最大流速）に比例し、配管径の２乗（断面積）に反比例することがわかります。流量で表現する場合は、圧力損失は、配管長と流量に比例し、配管径の４乗（断面積の２乗）に反比例します。
実際の配管の圧力損失は、これらに加え、配管の内表面性情、曲がり、弁、タンク、オリフィス、ノズルなど各種の要因がある。詳細は、「圧力損失」を参照してください。
Author: T. Oda
このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。