| |
 |
| |
 |
| 仠丂幙検曐懚懃丂楢懕偺幃 |
| 仠丂僄僱儖僊乕曐懚懃 |
| 丂丂仠丂儀儖僰僀偺掕棟丂惷埑偲摦埑丄悈摢偲偼 |
| 丂丂仠丂埑椡懝幐傪擖傟偨儀儖僰僀偺掕棟 |
| |
 |
| 仠丂幙検曐懚懃丂楢懕偺幃 |
| |
| 仠丂棳懱偺棳傟偱傕幙検曐懚懃偑側傝偨偮丅埑弅惈棳懱傪娷傓堦斒幃偼壓婰偱偡丅 |
| |
| 抐柺俙1傪捠夁偟偨幙検亖抐柺A2傪捠夁偟偨幙検 |
| 丂丂丂丂 兿1俙1U1儮T = 兿2A2U2儮T |
| 丂丂丂丂 兿1俙1U1 = 兿2A2U2 |
| |
| 仠丂旕埑弅惈棳懱偱偼 |
| 丂丂丂丂丂丂丂丂丂兿1 =兿2 |
| 丂丂丂丂丂丂丂 俙1U 1 = A2U2 |
| |
 |
| 仠丂僄僱儖僊乕曐懚懃丂儀儖僰僀偺掕棟 |
| |
| 乮侾乯丂棳懱撪偺丄棳慄忋偺僄僱儖僊乕偼堦掕偱偁傞丅 |
| 乮俀乯丂塣摦僄僱儖僊乕亄埑椡僄僱儖僊乕亄埵抲僄僱儖僊乕亖堦掕 |
| 乮俁乯丂埑弅惈棳懱偺応崌偼丄撪晹僄僱儖僊乕偑曄壔偡傞偑丄旕埑弅惈棳懱偱偼撪晹僄僱儖僊乕偼曄壔偟側偄偺偱丄撪晹僄僱儖僊乕偼柍帇偱偒傞丅 |
| 乮係乯丂旕埑弅惈棳懱偺掕忢棳乮塓偑側偄乯偲偡傞丅 |
| |
 |
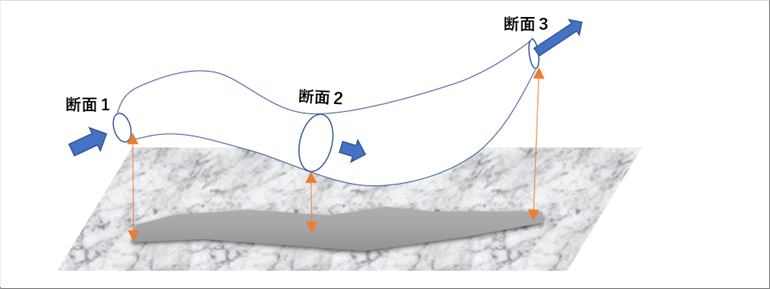
| 仠丂僄僱儖僊乕曐懚懃丂儀儖僰僀偺掕棟丂摦埑丄惷埑丄悈摢 |
| |
| 丂棳楬撪偱偼丄惷埑亄摦埑亄埵抲僄僱儖僊乕亖constant 偑僄僱儖僊乕曐懚偺朄懃偱丄儀儖僰僀偺掕棟偲偄傢傟偰偄傞丅侾俉悽婭偵儀儖僰僀偝傫偑採彞偟傑偟偨丅 |
| |
 |
| |
 |
| |
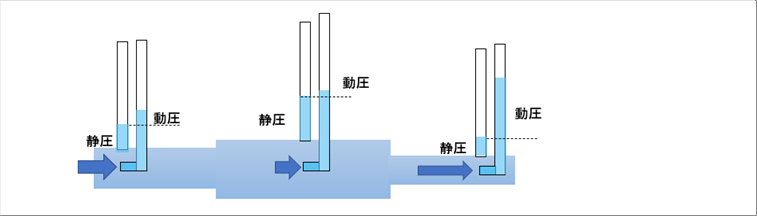
| 丂偦傟偧傟偺埵抲偵僈儔僗娗傪擖傟偰惷埑偲摦埑傪尒傞偲壓偺傛偆偵側傝傑偡丅 |
| |
 |
| |
| 丂惷埑偲摦埑傪悈摢乮僂僅乕僞乕僿僢僪乯偱昞偡応崌偼丄儀儖僰僀偺掕棟偺幃傪兿倗偱妱傞丅埑椡悈摢亄懍搙悈摢亄埵抲悈摢 = constant2 偑悈摢偺幃偲側傞丅 |
| |
 |
| |
| 丂惷埑丂P丂丂丂 亖亜丂埑椡悈摢 P/兿g |
| 丂摦埑丂0.5兿v^2 亖亜丂懍搙悈摢 0.5v^2/g |
| |
 |
| 仠丂埑椡懝幐傪娷傓儀儖僰僀偺掕棟 |
| |
| 丂幚嵺偺棳傟偵偼丄棳懱偺擲惈杸嶤側偳偵傛傞埑椡懝幐儮倛偑偁傝丄柍帇偱偒側偄掱搙偵戝偒偄応崌偑偁傞偺偱妋擣偑昁梫偱偁傞丅嚈倛傪偳偆昞尰偡傞偐偱偳偪傜偺幃傪巊偆偐曄傢傞偑丄偙偙偱偼懝幐僿僢僪偲偟丄億僀儞僩侾偐傜億僀儞僩俀偵棳傟偰偄傞応崌偼師偺傛偆偵側傞丅 |
| |
 |
| |
| 億僀儞僩偑摨偠悈暯慄忋偵偁傞側偳埵抲僄僱儖僊乕偑柍帇偱偒偰丄摨堦棳楬偵偁傞応崌偼丄懍搙傕摨偠側偺偱丄埑椡懝幐嚈倛偼丄師偺幃偲側傞丅乮徻嵶偼丄乽埑椡懝幐乿傪嶲徠偟偰偔偩偝偄丅乯 |
| |
 |
| 丂丂丂丂 |
| 丂丂丂丂丂兩丗僟儖僔乕偺杸嶤學悢 |
| |
| Author: T. Oda |
| 偙偺儁乕僕偼僄僋僙儖偱嶌傝丄excel2web偱html偲css傪帺摦嶌惉偟傑偟偨丅 |