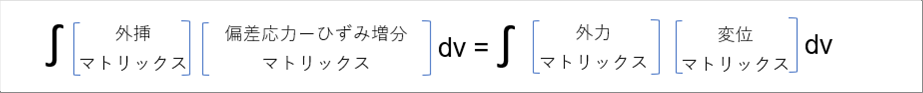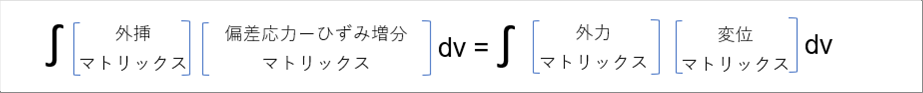有限要素法　Finite Element Method
●　有限要素法とは
有限要素法のメリット
有限要素法の注意事項
●　微分と有限要素法
●　有限要素法の適用
〇　構造解析への適用例
変数と方程式
境界条件
メッシュの種類
適切な要素形状
弾性変形と塑性変形
アスペクトレシオ、縦横比
メッシュの大きさ
計算結果の検証
発展
●　有限要素法とは
有限要素法の概要は「技術の話」の「数値解析」にも書きましたので参考にしてください。
有限要素法は、どの分野にも適用できて、自由度が高く、精度良く計算できます。そのためには、解析する分野についての知識が必要になりますが、各大学、研究機関、学会などからいろんなレポートが出ていますので、詳細はそちらを参照ください。例えば、東京大学生産技術研究所の塑性加工や伝熱についての講義レポートなどです。
ここでは、なるべく数式を使わないで有限要素法の特徴をかきたいと思います。特徴を４つに分けるとすると、次のようになると思います。
（１）微分方程式を近似的に解く解法の一つです。
（２）したがって、不可避的に誤差が発生します。
（３）解析する領域をメッシュ（要素）に分割します。
（４）その中に適用する方程式で連立方程式を作り、解きます。
（２）の誤差は、実機とそん色ないレベルまで小さくできます。
（３）のメッシュは自由ですが、大きさ、形状、個数などで結果に差が出ます。
（４）の要素内の方程式も自由です。例えば回帰式でも構いませんが、結果を左右します。
〇　有限要素法のメリット
こんな言い方は不適切かもしれませんが、（１）広く利用されているので、ブラックボックスとして使えます。
（２）複雑な形状のものでも高精度に解析できます。（差分法も複雑な形状の計算ができます。）
要素の平均的な数値が計算されるので、（３）要素の頂点、中間点などの数値を知りたい場所は、外挿で計算できます。外部から与えられる荷重などは要素の周囲に付加されるので、周囲の数値が計算できることは重要になります。
〇　有限要素法の注意事項
（１）まず、メッシュの形状、大きさ、個数を適切に決めなくてはなりません。（２）次に、メッシュ内に適用する数式は、元の微分方程式の代わりとなり、かつ、計算できる適切なものを選ぶ必要があります。（３）したがって、計算結果の吟味をする必要があります。
有限要素法をブラックボックス的に使う場合は、計算結果にいろんな指標が出力されると思いますので、それらを使って計算結果を吟味してください。例えば、構造解析などでは、応力分布のほかに「ミーゼス応力」などが出力されると思いますが、これらを使って評価すればいいと思います。（ミーゼス応力は、「材料力学」を参照ください。）
●　微分と有限要素法
差分法は、微分方程式をテイラー展開して直接近似しますが、有限要素法は、微分と有限要素法は数式上のつながりがなくてもかまわないと思います。
●　有限要素法の適用
〇　構造解析への適用例
構造解析では、有限要素法を使うことが多いと思われるので、例として、構造解析への有限要素法の適用を考えたいと思います。
〇　変数と方程式
数学の基礎ですが、変数と連立方程式の数が一致すれば、解が得られます。たとえば、変数が２個の場合は、2元連立方程式を解いて解を得ます。構造解析で知りたい変数は、物質内部の応力とひずみで、関係する方程式は、次の３種類です。
（１）　力のつり合い方程式
（２）　変位（位置の変化）とひずみの関係式
（３）　応力とひずみの関係式
これらの式は、各要素に適用されます。外部から付加されている範囲の力のつり合いから、ひずみが計算でき、ひずみから位置の変化がわかります。これを全要素にわたって計算すれば、知りたいことが計算できることになります。なお、それぞれの式は、「材料力学」で説明してあるので、参照してください。
〇　境界条件
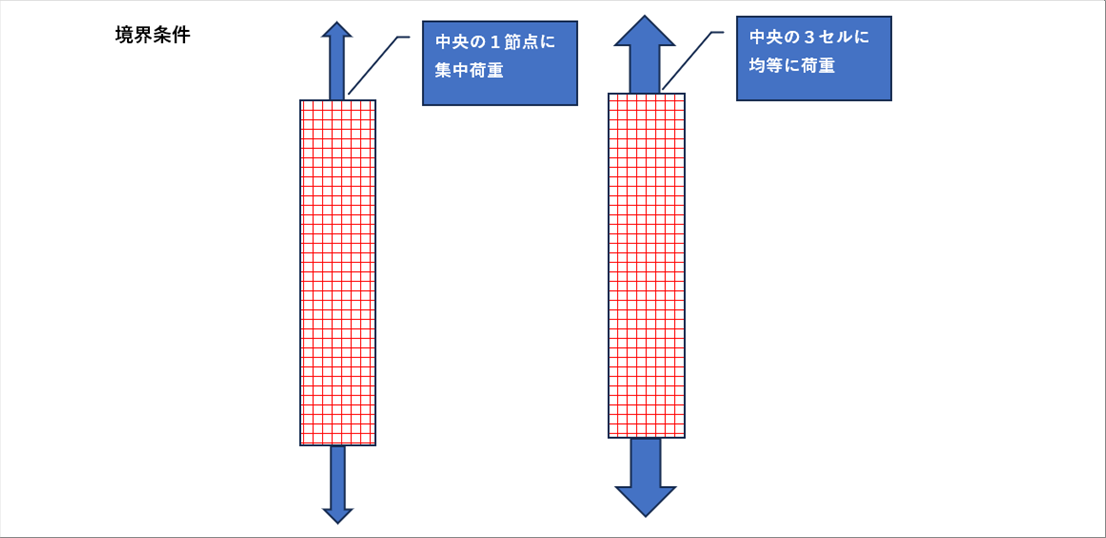
外部から付加される力の単純な例としては、引張試験のような、長い棒をつかんで引っ張る場合が考えられます。引張試験の一つの方法ですが、試験片の両端部をクランプし、一定のひずみ速度で、引張り、どれだけの荷重がかかるかを計測する方法があります。また、家が台風に耐えられるかどうかは、風力、方向などが与えられます。これらは、物体と外部との相互作用の境界に与えられる条件なので、境界条件とよばれます。
外力などの境界条件を、次の項目のメッシュのどこに、どのように作用させるかは非常に重要な要点になります。
「集中荷重」、「分布荷重」などは、境界条件を文字で表す場合は簡単で、「物体の端部から２ｃｍのところに下方向に１Ｎかかっている。」などの表現になりますが、有限要素法は、自由度が高いので、どのメッシュのどの場所にどの方向に作用させるのかを自分で選ぶことができます。したがって、文字では同じ表現でも、有限要素法での結果は必ずしも同じになるとは限りません。
〇　メッシュの種類
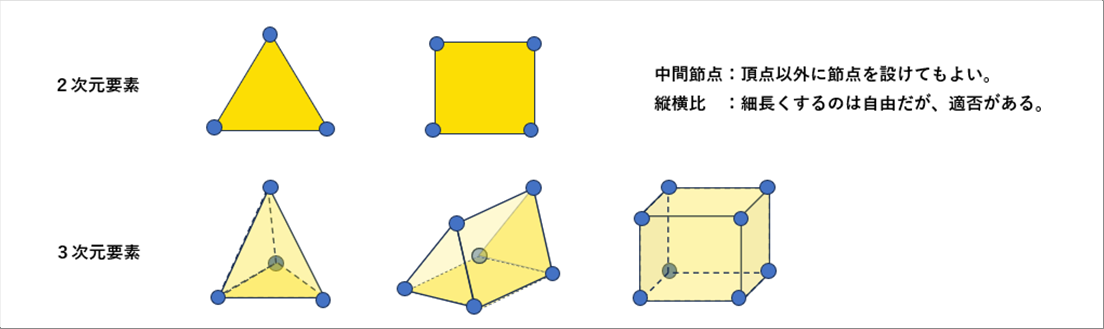
計算対象の次元は、１次元、２次元、３次元と３種類ありますが、実は、上で書いたような１次元の計算に有限要素法を使うことはほとんどありません。有限要素法では２次元、３次元を扱うことが多いと思います。２次元、３次元の要素には、下図のようなものがあります。
〇　適切な要素形状
〇　弾性変形と塑性変形
どの要素を使うかは計算者の自由ですが、弾性変形では三角形、塑性変形では四角形が主体のように見受けられます。
弾性変形：三角形
塑性変形：四角形
〇　アスペクトレシオ、縦横比
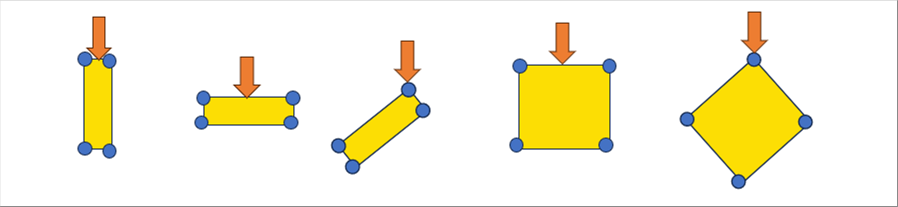
どちらかの方向に長い要素を使うことも、傾けた要素を使うこともできますが、場合によっては、計算結果が適切でない可能性もあります。
〇　メッシュの大きさ
メッシュ分割は、適切に行う必要があります。慣れていれば、１回で完璧な分割ができるかもしれませんが、あたりをつける目的もあるので、最初は粗いメッシュで計算し、より細かく知りたい場所を細分化するを、何回か繰り返す方法もあります。
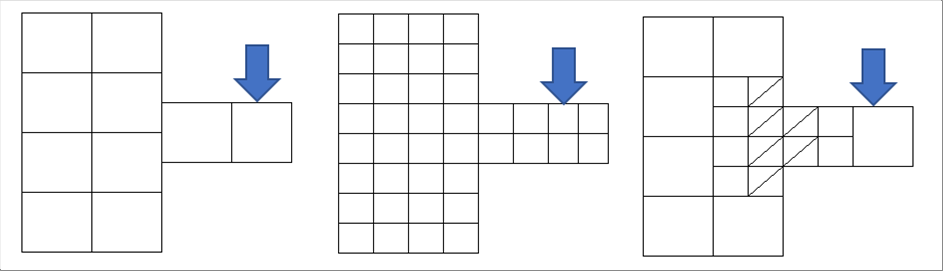
下の例で、どれが推奨されるかは一概に言えませんが、凸部分のある範囲だけ弾性変形して、ほかの部分は変形しない想定なら、一番右がいいかもしれません。
どこが変形するのかわからない場合は、まず一番左で計算してみて、凸のある部分の変形が大きいようだ、と、わかったら、その部分を細かくするのもいいと思います。
中央のように、全部の範囲を細かく分割して全部を細かく計算し、様子を見る方法もあります。
節点の座標は、全部でN個に分割する場合、２次元だとn番目の座標は(xn, yn),、３次元では(xn, yn zn)となります。
繰り返し計算がしやすいようにメッシュに番号を振ります。例えば、境界条件が与えられる要素が連番になるようにするなどです。
〇　計算
要素内に適用する連立方程式を解きます。縦横３セルずつ、計９セルでも、頂点が１６個あり、２次元の場合は未知数が３２個あることになるので、３２元連立方程式になります。下の絵では、５６０元連立方程式になります。連立方程式の係数と境界条件を行列（マトリックス）で書いて、線形代数の公式を使うと解きやすいので、有限要素法では、マトリックスがよく出てきます。
「要素に適用される式を全領域にわたって計算する」のですが、数学的には体積積分と言います。体積全部にわたって、要素ごとの積分を合算するので、要素内の式は、簡単に積分できる形になっていると便利です。基本的な微積分は「技術の話」「微積分」を参照ください。
簡単に積分できない関数を内部関数とする場合は、数値積分を利用することもできます。数値積分はいろいろありますが、「数値解析」「数値積分」のガウス・ルジャンドル法を参照ください。誤差はありますが、4次程度まで計算すると誤差は十分小さくできるようです。（ガウス・ルジャンドル法詳細は、WikiPediaなどを参照ください。）
最後になりますが、要素内に適用される式は、要素の（ある意味)中央で、要素内で平均的に適用されるので、節点の数値にするためには、外挿します。境界条件は、節点にかかるので、外挿は必須と言っていいと思います。このため、有限要素法の式では、外挿マトリックスが行列積されている式が見られます。
〇　計算結果の検証
例えば、各メッシュの頂点の位置が計算結果として得られた場合、位置の変位分からひずみが計算でき、応力ひずみ線図で応力がわかります。応力X面積で荷重が計算でき、荷重Xトルクアームで動力の計算ができます。
これらの計算結果の評価は、実際に計測できる数値と比較するのが一般的だと思われます。
ひずみゲージで、代表点の応力、ひずみを計測して比較する、工具の荷重と動力を比較するなどの方法があると思います。
〇　発展
数学的にあっているかどうかわかりませんが、構造解析などの場合、説明を式で書くと次のようになると思います。
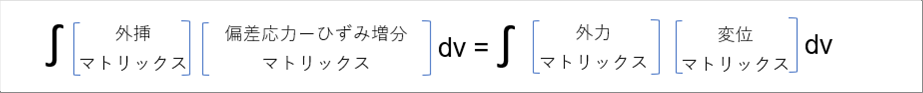有限要素法は、構造解析以外にも、熱流体の熱伝達、熱伝導計算、圧延などの塑性加工の計算などでも活躍しています。これらの微分方程式も解析的には解けないからです。要素内に適用される式と境界条件がかわります。詳細は「熱力学」「流体力学」「塑性力学」を参照ください。
構造解析は、CAD、CAEなどのプログラムから直接利用できるものもあるようです。メッシュ分割も自動的にやってくれるものもあるようですが、結果の是非の判断はしたほうがいいと思います。
構造解析をして、永久変形（塑性変形）するかどうかの判断は「塑性力学」の「基礎」で説明した降伏条件で推定可能です。最大主応力説、トレスカの降伏条件、ミーゼスの降伏条件、相当応力説などがありますが、解析に適切と思われる説を採用して判定できます。
有限要素法の自由度の高さを利用して、故障解析（Failure Analysis）にも適用できると思います。例えば、通常の状態では壊れない設備が壊れたとき、外力の何が変わると設備が変形（もしくは破損）するのか、などは、境界条件の外力の負荷方向や摩擦係数を変えて設備のどの部分の応力が変わり、降伏条件になるのか、などが計算できると思います。
Author : T. Oda
このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。