差分法とは Difference Method
●　差分法、差分法のメリットとは
●　微分法と差分法
微分法と差分法　（１次元）
1階前進差分法の誤差
1階微分の差分での表し方
2階微分の差分での表し方
●　エクセルで差分法を計算
差分法の表計算結果
３D表示
●　差分法、差分法のメリットとは
微分方程式は、無限級数に展開すれば、誤差なく表現できますが、「無限」と名の付くものは計算できないので、有限個を計算に使い、残りの部分を誤差にします。例えば、計算に使う有限個を２次までとし、3次以降の高次部を誤差として、この誤差を許容できるほど小さくできれば「使える」微分方程式の解法になります。差分法の最大のメリットは、解けない微分方程式でも、ある時点の分布状態がわかれば、どう変化していくかがわかることです。つまり、誤差を十分小さくできれば、実用的に問題ないレベルのシミュレーションを、比較的手軽に行えることだと思います。
具体的には、差分法は、微分方程式の近似解法のひとつで、微分方程式を直接テイラー級数展開して、文字通り差分形式（Δｘなど）で解くので、時刻０の空間的な分布状態が分かれば、微少時刻後の状態が計算機で数値計算でき、あとは芋づる式に状態が計算できる。（陽解法のひとつ。）ただし、無限級数の使わなかった部分が誤差となる。と、いうものです。有限要素法とちがい、専門知識に基づく近似式がなくても解が得られます。
●　差分法と微分法
微分方程式は、我々の先輩方がいろいろ研究されているおかげでいろいろ利用させていただけます。ここでは、微分方程式をどうやってシミュレーション計算に利用するのかを書きたいと思います。
下の絵は、上面に高温部がある単純な加熱炉の模式図です。そこに左から入った物体の温度は、炉内を右に移動するにしたがって上昇します。
模式図にあるように、上面に既知の温度分布を持つ加熱板があり、左下から四角の金属片を入れて右方向にある速度で動かしたときの、金属片の位置ごとの中心温度が知りたいとします。
加熱板によって熱せられるもの、すべての計算をして、金属片の温度の計算をします。この方針は、それぞれの知りたい内容によって変わり、熱関係であれば輻射熱、対流による伝達熱が金属片に対する入熱エネルギーになります。この熱エネルギーは、金属片の周囲４辺から金属編内部に伝導します。
温度変化の計算をするので、熱エネルギーの１階微分と2階微分が必要になります。微分方程式は、熱力学を参照ください。数値解析のページでは、それらの微分方程式は、運動方程式と似ているという理解だけでも大丈夫です。
運動方程式Ｆ＝ｍαは、物体の加速度αに質量ｍをかけたものが作用する力Ｆになることを示しています。物体の位置の１階微分が速度で、位置の２階微分が加速度です。
●　差分法と微分法　（１次元）
３次元で考えていくと複雑なので、１次元の場合を考えたいと思います。２次元、３次元の場合でも１次元と全く同じに考えればいいので、２，３次元の場合に思いいをはせつつ、１次元で見ていきたいと思います。
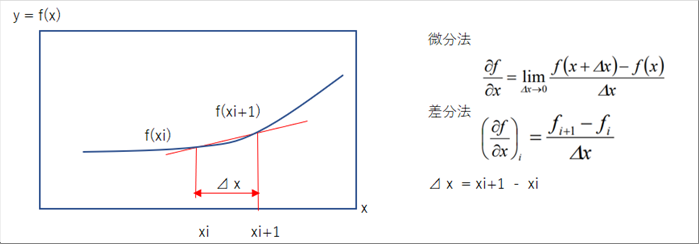微分は、�凾�をゼロに持っていくので誤差は発生しませんが、すべての微分方程式の解が得られるわけではありません。
差分は、�凾�が誤差になります。�凾�を小さくすれば、工業的に問題ないレベルの誤差になります。計測の誤差、素材の寸法誤差などもあるので、シミュレーションにも許容誤差があるはずです。もとの微分方程式が解けなくても解が得られるのが最大のメリットになるので、プログラムを組んでもいいし、�凾�ごとのエクセルの表にして表計算を使っても計算ができます。
なお、�凾�など、ある区間で区分することを離散化するというが、空間、時間を有限に分割することと思えばいいと思います。
●　１階前進差分の誤差
fxが観測数値で、fx+1が未知の数値です。「前進」とは、ｘの次という意味で、ｘの後ろfx-1もあり、こちらは「後進」と言いますが、あまり気にする必要はありません。
微分法は未知数の�凾�をゼロにするのでfxだけの関数です。したがって、微分方程式が解ければ誤差がない解がが得られますが、解けないのものが多いです。差分法は、ｆｘと�凾�でその次のfx+1を計算できますが、�凾�が残るので誤差になります。したがって、�凾�を評価してできる限り小さくする必要があります。
fx+1を計算するには、テイラー展開を使います。テイラー展開は、ある関数の未知の値fx+1を、既知のfxからの傾きに距離をかけて算出します。ただし、傾きと距離だけでは、ほしい値fx+1に対して過不足が発生します。この過不足を、無限に続く高次の微分と影響係数で補正します。無限に続く補正なので、最後は誤差（過不足）がなくなるということだと思います。（詳細は、数学参照）
誤差で重要なのは、3次以降の補正項は、�凾�でくくれるので、�凾�の関数だということです。�凾�を小さくすれば誤差が小さくなりそうなのはグラフからも明らかですが、テイラー展開の式で�凾�の関数であることが証明されたことになります。
●　1階微分の差分での表し方
実際の解が欲しいシミュレーションでは、無限に計算することはできません。今はコンピューターが手軽に使えます。どこで打ち切らなくてはならないというルールはないと思いますが、昔から使われている所だと、2階微分までは計算し、3階微分以降を誤差にします。この程度であれば、エクセルのセルを使った計算も可能になります。
テイラー展開の２次の項までを計算することにしています。まず１次の項を差分で表す方法から考えたいと思います。
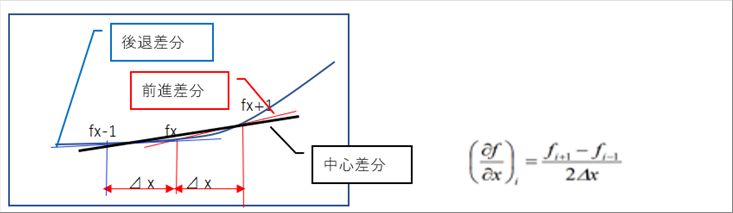３種類の差分のどれを使わなくてはならないという決まりはないと思いますが、中心差分がおすすめです。上のグラフィックの式は、中心差分の式です。
●　2階微分の差分での表し方
１階微分は傾きで、２階微分は傾きの傾きになります。2階中心差分は、前進１回差分と後進一階差分の�凾�での変化で定義します。（ほかの表現は割愛します。）
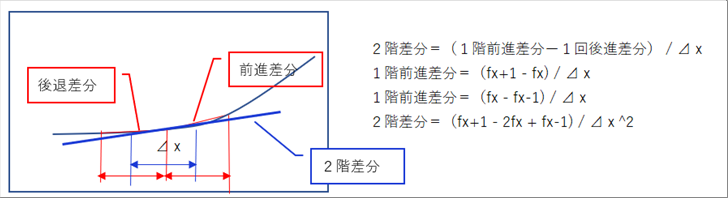●　差分法でのシミュレーション
以上で、差分法で１階微分と２階微分の式が求められました。計算手順は簡単で、微分方程式の１階微分と２階微分を差分の式で置き換え、fx+1= の式に変形するだけです。
解析したいのは、ある物体の時間的、空間的変化で、微分方程式はそのようにできていると仮定します。例えば、熱伝導方程式をもっとも単純化すると、温度の時間変化は、位置の２階微分に比例する式になります。手順をまとめると下記のようになります。
１）微分方程式を差分法で書き直す。
２）次に、時刻＝０の各位置の数値を初期条件とする。
３）微小時間�凾狽ｲとに計算を繰り返す。
４）出力。
細長い棒のようなものは１次元、ある断面をトレースする場合は２次元、ある部分もしくは全体をトレースする場合は３次元になります。
温度分布が計算結果として得られる場合などは、画面上で３D表示をしたほうが見やすい場合があります。その場合は、得られたデータを３D化する計算を計算の最後に追加すると簡単に３D表示ができます。
●　エクセルで差分法　（詳細「温度計算」参照）
ー　差分法の表計算結果
エクセルのセルでシミュレーションができると書いたのは、セルにタイプする式が2階微分までと比較的短いので、セルに式をタイプすることが可能になるという意味です。エクセルのセルには半角で約32,000文字入るようなので、相当長い式でも問題ありませんが、短いほうがいろんな意味で便利です。
計算時には、計算範囲の境界の扱いに注意が必要です。中心差分を選んで計算をする場合でも、境界部は範囲のヘリなので、前進差分か後進差分のどちらかを採用する必要があります。
下のエクセルの表は、円柱座標で丸鋼片の昇温状態を計算した結果です。詳細は、「温度計算」を参照してください。
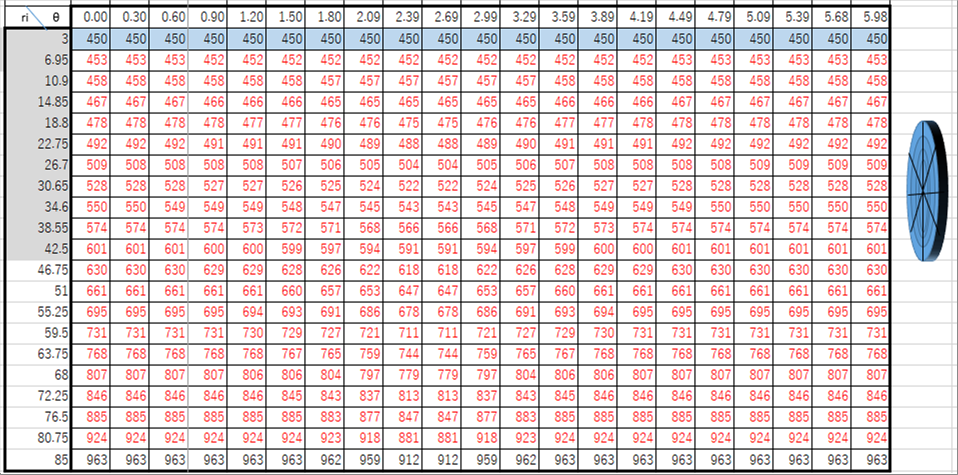ー　３D表示
エクセルで３D表示をする場合は、球面座標変換をすれば計算結果を３軸で自由に回転できますので、非対称な計算結果でも全体を把握するのが容易になると思います。
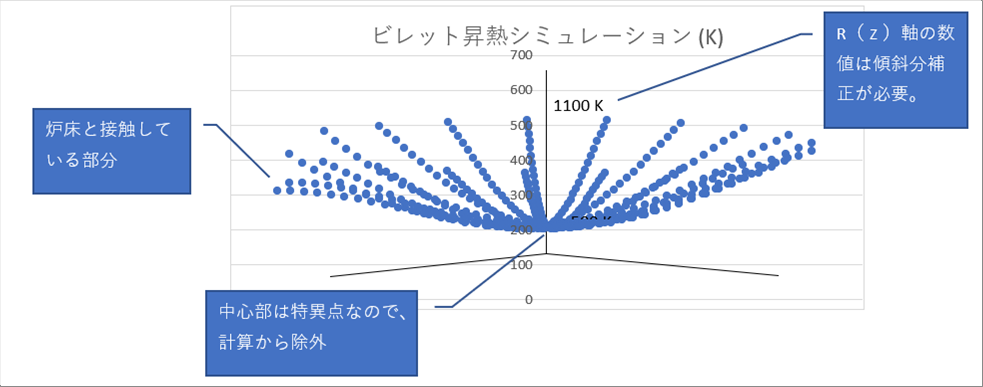
下のグラフは、エクセルで計算した上の表を３Dで表示させた例です。計算方法詳細は、「３D回転」を参照ください。
グラフのコメント３点を若干補足させてください。
円柱座標では、中心部が特異点になるので、計算上は中心から3mm離れた位置から丸鋼片の外周部までの計算をしました。
また、丸鋼片を置く床の温度は、周囲の雰囲気温度より低いと仮定しているので、３Dグラフの左側が低い温度になっています。計算では、床は耐熱煉瓦でできていると仮定して、熱伝導係数などは丸鋼片とは違う数値を使っています。
３Dグラフの縦軸は変換前の数値です。縦軸も画面手前に倒れているので、数値も変換する必要があります。縦軸の500と600の間にタイプした「1100 K」が変換後の数値です。
Author: T. Oda
このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。