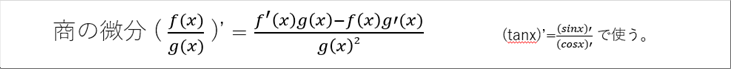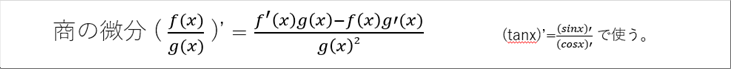| |
|
 |
|
| |
|
 |
|
| ● 微積がストーリーなのは |
|
| ● 積分の例 断面二次モーメント |
|
| 三角関数の4乗の積分 |
|
| 半角の公式 三角関数の2乗以上が出てきた際の定石 |
|
| 変数の置換と合成関数の積分 cos2θの積分 |
|
| 三角関数の加法定理(詳細は最後の項参照) |
|
| ● 合成関数の微分 |
|
| 商の微分 |
|
| ● サイン、コサインの微積分の公式と覚え方 |
|
| 三角関数の微分積分の公式まとめ |
|
| ● 対数の微分 1/x |
|
| ● 指数関数の微分 (a^x)' = (a^x) log a |
|
| ● 積分の例 熱伝導方程式の解 |
|
| |
|
| 〇 三角関数の加法定理 |
|
| cos ( a 土 b ) = cos a cos b 干 sin a sin b |
|
| sin ( a 土 b ) = sin a cos b 土 cos a cos b |
|
| tan ( a 土 b ) = ( tan a 土 tan b ) / ( 1 干 tan a tan b ) |
|
| |
|
 |
|
| |
|
| TSCが数学のコンサルをすることはありませんので、詳細に立ち入ることはありません。微積分の公式が使えれば理論は全部フォローできますが、考え方と計算方法の流れがわかるようにまとめてみました。流れを重視してまとめたので、ストーリーに入れています。数学的な説明内容をご存じの方はスキップしてください。 |
|
| |
|
| 微積分では、三角関数、指数関数が忘れがちだと思います。例えば、円形断面の部材の剛性、変形を計算する際に使う断面二次モーメントの計算に使われています。ただし、変数分離法で伝熱方程式の解析解を求める場合に使っている積分は高度なので計算結果だけでいいと思います。 |
|
| |
|
| なお、三角関数の微積分以外の公式は、単位円を描いて図で見て考えるのが一番手っ取り早いと思います。参考として加法定理を載せました。 |
|
| |
|
 |
|
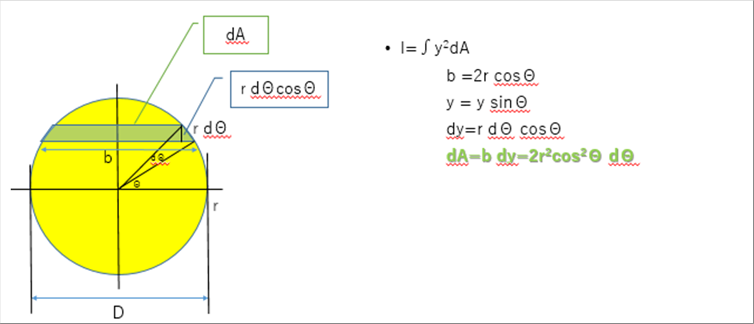
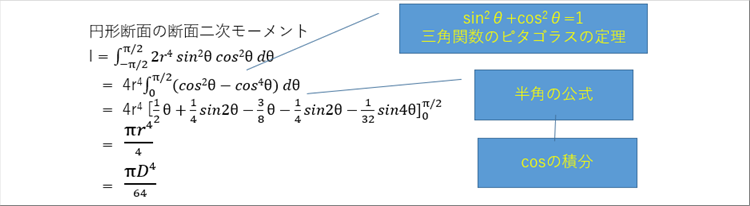
| ● 積分の例 断面二次モーメント |
|
| |
|
| 相当多数の微積分の公式を使っている例として、円形断面の断面二次モーメントを取り上げてみます。円形断面の断面維持モーメントは、極座標系を使い、微小区間で断面二次モーメントの定義式を使い、面積積分して求めます。 |
|
| |
|
| x軸周りの断面二次モーメントの定義式は、yの2乗を積分します。yをrとθで表して定義式に代入すると次のようになります。 |
|
| |
|
 |
|
| |
|
| r、θの場所の微小面積の幅bとyを定義式に代入すると三角関数の4乗の積分が必要になります。 |
|
| |
|
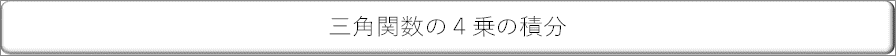 |
|
| ● 三角関数の4乗の積分 |
|
| |
|
| 三角関数の微積分の公式は1乗のものだけですが、円形断面の断面二次モーメントを求める際には、三角関数の4乗の積分が必要になります。 |
|
| |
|
 |
|
| |
|
| 上の式では、COSθの4乗は、三角関数の半角の公式を適用して1乗にしてから積分してます。三角関数がn乗になっていたら、2乗づつ半角の公式を使って1乗にして計算するのは三角関数の計算の「定石」です。 |
|
| |
|
 |
|
| |
|
 |
|
| ● 半角の公式 三角関数の2乗以上が出てきた際の定石 |
|
| |
|
| 三角関数の2乗以上が出てきた際の定石は、半角の公式を使って1乗にすることで、三角関数を解析で扱う際の、もっとも重要な手法の一つです。 |
|
 |
|
| |
|
 |
|
| ● 三角関数の加法定理 |
|
| |
|
| 加法定理は、円を描くと簡単に理解できます。円周上の2点間の距離は、2点の角度の和(差)を保ったまま円周上で回転しても常に同じという円の性質を数式で表現したものです。 |
|
| |
|
| 加法定理だけ覚えれば三角関数関連の公式は微分も含め全部導出できますが、半角の公式は覚えておいて損はないと思います。詳細は、最後の項を参照ください。 |
|
| |
|
 |
|
| ● 変数の置換と合成関数の積分 cos2θの積分 |
|
| cosαの積分は公式がありますが、 cos 2θの積分の公式はありません。 |
|
| |
|
| 公式を使うためには、「2θ=α」とおきますが、これを変数の置換といい、公式と変数置換を同時に行います。同時に行うことは、その二つを合成しているということなので、これを利用した積分を合成関数の積分といいます。 |
|
| |
|
| 公式を使うための変数の置換、合成関数の微積分は非常によく使います。 |
|
| |
|
 |
|
| |
|
 |
|
| ● 合成関数の微分 |
|
| |
|
| 三角関数の例だと、cos(2θ)も合成関数です。 |
|
| y=f(u)の変数uをu=g(x)と置換するとき、y=f(g(x))を合成関数という。 |
|
 |
|
| |
|
| 使い方が簡単で使うところが多いので、個人的には微積分の中で一番好きな公式です。通分してはいけないのでしょうが、数学の専門家でない身なので、そのほうが覚えやすいですし、少なくとも思い出しやすいです。 |
|
| |
|
 |
|
| |
|
| 分母分子に同じものをかけるのがミソだと思います。公式は通分ではないということですが、limの中では通分を利用してますよね。。。 |
|
| |
|
 |
|
| ● 商の微分 |
|
| |
|
| tanθの微積分で使います。tanθ = sin θ / con θ |
|
| 小の微分の公式は下記です。これは、微分の定義である導関数を変形すると導くことができます。 |
|
| |
|
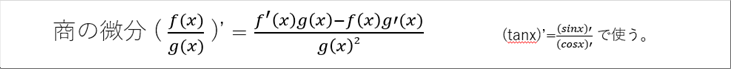 |
|
| |
|
 |
|
| |
|
| 同じものを引いて足すのがミソだと思います。 |
|
| |
|
| 同じものを分母分子にかける、同じものを引いて足すは、微分方程式でもよく使われています。 |
|
| |
|
| また、運動の式では、「連続の式」という名前の式がありますが、例えば、水は流れているときに切れて真空にならないということです。式では、x方向、y方向、z方向の流速を足したらゼロという式です。 |
|
| |
|
 |
|
| ● サイン、コサインの微積分の公式と覚え方 |
|
| |
|
 |
|
| |
|
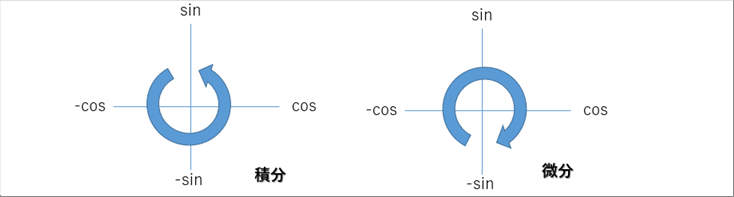
| sinとcosを下の絵のようにかくと、積分は反時計回り、微分は時計回りの関係になっている |
|
| |
|
 |
|
| |
|
 |
|
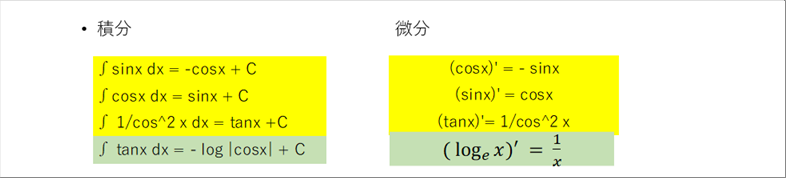
| ● 三角関数の微分積分の公式まとめ |
|
 |
|
| tan x の微分は sin x、cos x に分解して分数の微分の公式で証明できる。tan の積分に戻らないで cos x の式になります。 |
|
| |
|
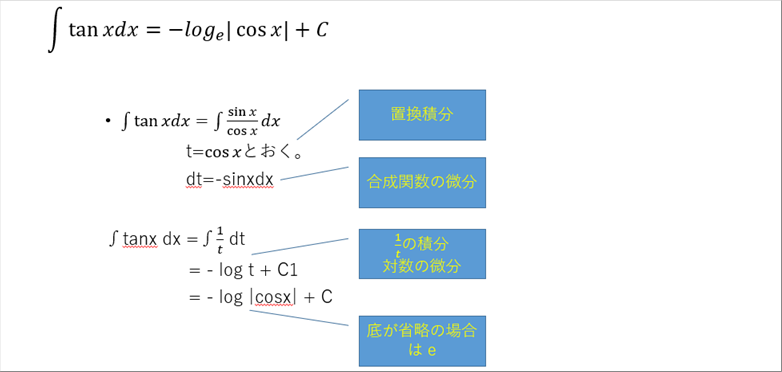
| tan x の積分はsin x 、cos x で書き換え、cosx=t で置換計算すると、単純に 1/t の積分になる。自然対数の微分が 1/t なので、上の式が成り立つ。 |
|
| |
|
 |
|
| |
|
 |
|
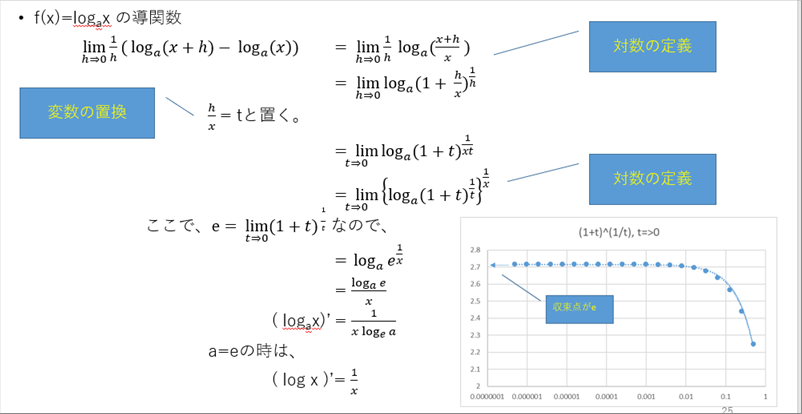
| ● 対数の微分 1/x |
|
| |
|
| 数学が趣旨ではありませんが、重要なので記しておきます。 |
|
| |
|
 |
|
| |
|
 |
|
| ● 指数関数の微分 (a^x)' = (a^x) log a |
|
| |
|
| 指数関数の微分は指数関数です。 |
|
| |
|
 |
|
| |
|
| xのべき乗とは違った式なので、覚えにくいですが、忘れたら導関数から導くことができます。 |
|
| |
|
 |
|
| ● 積分の例 熱伝導方程式の解 |
|
| |
|
| 熱伝導方程式 ∂u/∂t=α ⊿u (⊿:ラプラシアン)は通常は解析的に解けません。(詳細熱伝導参照) |
|
| |
|
| 熱伝導方程式が、その変数だけの式の積 u(x,t)=T(t)X(x) で表現できる場合に限り、例外的に解析的に解けます。物理現象としては単純すぎると思いますが、このくらいでないと解析解は得られないということです。 |
|
| |
|
 |
|
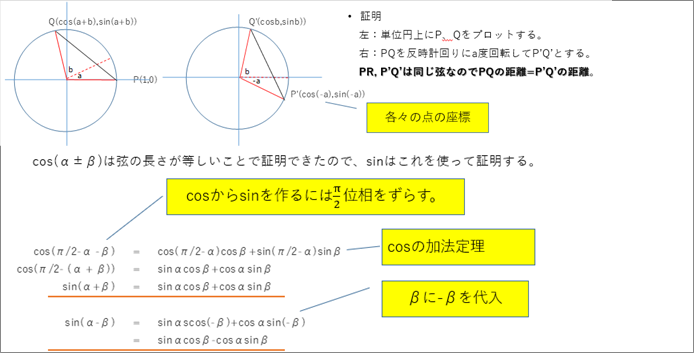
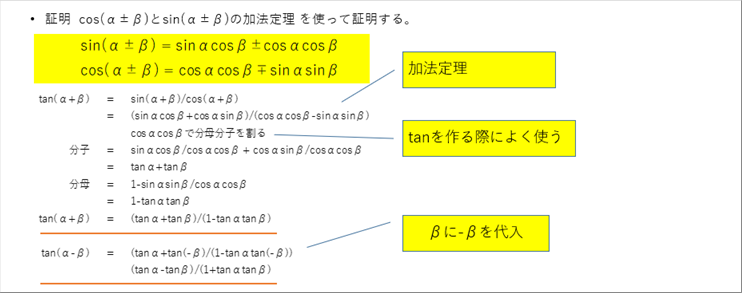
| ● 三角関数の加法定理 |
|
| |
|
| 割愛すると書きましたが、興味のある方が参照できるように単位円を使った証明を載せておきます。 |
|
| |
|
| cos ( a 土 b ) = cos a cos b 干 sin a sin b |
|
 |
|
| |
|
| sin ( a 土 b ) = sin a cos b 土 cos a cos b |
|
 |
|
| |
|
| tan ( a 土 b ) = ( tan a 土 ttan b ) / ( 1 干 tan a tan b ) |
|
 |
|
| |
|
| |
|
| |
|
| |
|
| Author: T. Oda |
|
| このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。 |
|